IV.4. Parallelogramme - Umfang: Unterschied zwischen den Versionen
| Zeile 215: | Zeile 215: | ||
9. a=31m, b=56m: { 174m } | 9. a=31m, b=56m: { 174m } | ||
| − | {Ein rechteckiges Grundstück hat eine Länge von 120m und eine Breite von 40m. Wie groß ist der Umfang? | + | {'''Ein rechteckiges Grundstück hat eine Länge von 120m und eine Breite von 40m. Wie groß ist der Umfang?''' |
| type="{}"} | | type="{}"} | ||
{ 340m } | { 340m } | ||
| − | {Wie groß ist der Umfang wenn die Länge 80m und die Breite 15m sind? | + | {'''Wie groß ist der Umfang wenn die Länge 80m und die Breite 15m sind?''' |
| type="{}"} | | type="{}"} | ||
{ 190m } | { 190m } | ||
</quiz> | </quiz> | ||
| − | '''4. | + | '''4. Ordne die Rechtecke nach der Größe ihres Umfangs. Beginne mit dem kleinsten Umfang. Klicke auf die Rechtecke um deren richtige Größe zu erkennen.''' |
<iframe src="http://LearningApps.org/show?app=60685" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | <iframe src="http://LearningApps.org/show?app=60685" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
<br /> | <br /> | ||
| − | '''5. | + | '''5.Welchen Umfang besitzt das Parallelogramm mit...''' |
<br /> | <br /> | ||
| Zeile 244: | Zeile 244: | ||
| | ||
| − | '''6. | + | '''6.Vervollständige den Satz.''' |
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
Der <strong>Umfang</strong> einer <strong>Figur</strong> ist die <strong>Länge</strong> ihrer <strong>Randlinien</strong> .</div> | Der <strong>Umfang</strong> einer <strong>Figur</strong> ist die <strong>Länge</strong> ihrer <strong>Randlinien</strong> .</div> | ||
Aktuelle Version vom 2. Dezember 2013, 14:57 Uhr
IV. Geometrische Grundbegriffe:
Erklärung
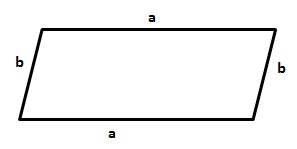
"Vierecke, bei denen gegenüberliegende Seiten parallel sind heißen Parallelogramme."
Jedes Quadrat, Rechteck und jede Raute sind Parallelogramme.
Umfang: "Der Umfang einer Figur ist die Länge ihrer Randlinien."
Ein Parallelogramm mit den Seitenlängen a und b hat den Umfang U:
U = a+a+b+b
U = 2a + 2b
U = 2(a+b)
Aufgaben
4. Ordne die Rechtecke nach der Größe ihres Umfangs. Beginne mit dem kleinsten Umfang. Klicke auf die Rechtecke um deren richtige Größe zu erkennen.
[ LearningApps.org is not an authorized iframe site ]
...Breite: 21cm , Länge: 29cm (! 87) ( 100) (! 54)
Der Umfang einer Figur ist die Länge ihrer Randlinien .
|
IV. Geometrische Grundbegriffe:

