IV.9. Schrägbilder: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
Zeile 185: Zeile 185:
 
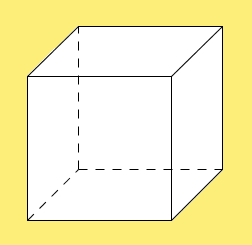
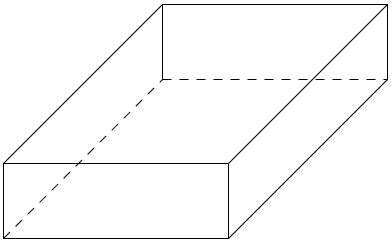
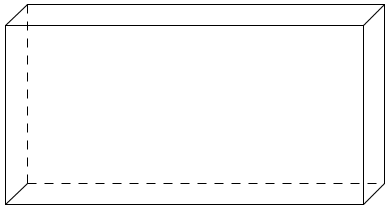
: Als Schrägbild bezeichnet man einen Körper, der auf einer ebenen Fläche (z.B.einem Blatt Papier) aus schräger Perspektive 3-dimensional dargestellt wird.
 
: Als Schrägbild bezeichnet man einen Körper, der auf einer ebenen Fläche (z.B.einem Blatt Papier) aus schräger Perspektive 3-dimensional dargestellt wird.
  
−
 
+
[[Datei:Schrägbild Würfel.jpg]]
−
:: <ggb_applet width="190" height="203"  version="4.0" ggbBase64="UEsDBBQACAgIAHB5jEIAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIAHB5jEIAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Vrbbts4EH1uv2Kg59oWdXdht2jSpg2Qtguku1jsGyXRMmNZ0oryrejH75CUZDtKutV2EbgG4vA2nOGcM8OLk8nr7TKFNSsFz7OpQYamASyL8phnydRYVbNBYLx+9XySsDxhYUlhlpdLWk0NR0ryeGqw0I/j2GIDYrvmwLG8YBBafjAwvXBmubOIRUFoAGwFf5nln+iSiYJG7DaasyW9ySNaKcPzqipejkabzWbYmBrmZTJKknC4FbEBuMxMTI268hLVHU3a2ErcMk0y+vPjjVY/4JmoaBYxA6QLK/7q+bPJhmdxvoENj6v51LBMz4A548kcfbLJ2ICRFCoQkIJFFV8zgVMPmsrnalkYSoxmcvyZrkHaumNAzNc8ZuXUMIdj3wx82w88x/R9zzcgLznLqlqU1CZHjbLJmrON1ipryqBjQJXnaUilQvj2DSzTMuGFLIguLCw8Tw+Zus+0dWHpwtGFq2UcPd3Roo6WcbSMYxuw5oKHKZsaM5oKBJBnsxLJa9ui2qVMrafu2DtPXqBPgn9FYdvEKNGIY79pvpAfDz+OHBgdO0kOrFblqqfRxiQZ9zBp/ZSjdmPTeshNy33ETe87RrXfP+Sne2ATTakf9elYtL/n5n2Luv1zBj3nSVycjJpUmdTZAWIuZevoqdhSyHyxx+COZdgTcDE3PB+j3AUyxsK3ALMBiAuOi00SgCdLH2wfBxywIQApR2xQyeEG+MvxlTIPXFQme33MSSBoyAHXBqJyygHMJFB5iTlq2SjhuuDiJGmeWFKF7YHjYcsOwME1ypT0CQraOBHbaN4Cm4AtJxMfLA88qY84MtW9QC4dVVrgmeARqRCzGjNaZzPKB2BLb7waLp4Vq6qGqEY9WsYNXFVetN0ojhvSftfTG9TRpvhsktKQpXhO3EoqAdY0ldwpS7M8q6BNDt2XlLSY80jcsqrCWQLu6Jre0Iptr1BaNLaVbJRn4rcyry7zdLXMBECUp2azUKyTg7q1dyZP7YMB53DAPRjwDur+g3ZzHIGVYGg/L0UjTuP4Wkrs9waE8nOW7i5KRhdFzo/dmIzUkTNhqyjlMafZHxit0orEBZoTSO1XzQlEfLdZSF7GtzuBIQzbv1iZYwKQoevYvjceW64TWCgJOz1iEXPo26bvuYEf2JaPp5iIqMw9ezwcu5bvOfgJxq6DqbWrhxxziGdCYHmeQ7yxpc2ydcsO3bK9o0nJ2ziR9WtxkadxO6xcv6RFtSrVvQE3xlI69CZLUqbCQ221eChHizDf3urstrWuL7sCW3WQhImCHHBfsFz0MKnLUJdKRq6slTKVjKkk2kDjcTtO0DUpocpQl0oKI1cvrfaUNF4SszHDhdrNTOM4Z1TcT42tAauMVze6hfnDo0XtK9EzPq2WIWvD51gpeVhpf52T0b34mixYmbG0Dmckc5WvhM7Og0iPWcSX2NQDjcuSr99xAbo3ZknJmoWn6lKmETucoyO1061UXZX58jpbf8FguLeAyahZ5UREJS9kzEGIZ8CC7cMq5oLiERIfzpP5h65H8qhAeCoJDWbmqprnpbp34YaCpUy7lC3xmgWVii8Voi3Mb9T1TeIJeXiHe9p9HvaM4fiDwabCkqbFnMo7Xu11SnesPMJB6fuYx/fRQfCVC5jhhSa3YEzHhV4wVgpUp/LpaIdCuAVsp8ZAXdZ39aX9qy717VX6KpNM23QOe+8RhdGjYfoXwC7OCTDnCQC7PAPArCfE6+0Z4fUUCfnuDPCya7ysJ8Dr6ozwcp8Ar/dngJf5hHh9OCO8/q98jPLlkmYxZOrdf8sS2W/sX6LUlDcxoERu/xqaVdUMUK2t1tFBX9TaGnhpF//6mww9fuDwY/ib/x39LoZ2jeHAbnW1D44Kn8GLjAmhXkpV/f5RlQ88jlnWvqPZ35meIvQjgC+LlEe8atFKJZ3XWYVPAqbuxN2b/oKxQr6xPmdfSpoJ+QWuljl4QfSi7PIxysJ+lIUnQlmzrZoNZd7ZUVZn2UWHsqgfZdGJUDbocHZ+aXahObvscBb34yw+Ec46OyOxzpWz9x3OWD/O2Ilw1vmOYeCeHWfvNWdXHc5m/TibnQhn3Tw7P86uNGfvOpwl/ThLToSzznE2PjvKLh9Ls3k/yuYnQll3azy/4+ztY2nG+3HGT5UzcnaU1Tf9Dx3K7vpRdneqlP1omhH31yHtw2N5tuhH2uJESOtcQX7wRf0Lcta96qf9OEtPhLPOk9r8tTgbHf5lWP3zRf1/hK/+AVBLBwiCwErplwYAAOQoAABQSwECFAAUAAgICABweYxC1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAgIAHB5jEKCwErplwYAAOQoAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAALgcAAAAA" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />
+
 
<br/>
 
<br/>
 
:: Schrägbild eines Würfels
 
:: Schrägbild eines Würfels

Version vom 27. Oktober 2013, 10:04 Uhr

Erklärbär.PNGP-Seminar/Mathematik 2010-12
Hauptmenü
-----------------------------------------------------------------------------------
















 

IV. Geometrische Grundbegriffe:  

1. Geometrische Körper - 2. Geraden - 3. Abstände - 4. Parallelogramm - Umfang - 5. Kreise - 6. Winkel - 7. Achsensymmetrie - 8. Netze geometrischer Körper - 9. Schrägbilder


Erklärung

Als Schrägbild bezeichnet man einen Körper, der auf einer ebenen Fläche (z.B.einem Blatt Papier) aus schräger Perspektive 3-dimensional dargestellt wird.

Schrägbild Würfel.jpg

Schrägbild eines Würfels




Vorgehensweise zum Zeichnen eines Schrägbildes

1. Zeichne die Vorderfläche in wahrer Größe
2. Zeichne nach hinten verlaufende Kanten (Tiefenkanten) um 45° geneigt, um einen dreidimensionalen Effekt zu erreichen. Konstruiere die Kanten zudem nur halb so lang wie das vorgegebene Maß.
3. Zeichne nicht sichtbare Kanten gestrichelt um den räumlichen Eindruck zu verstärken.




  Aufgaben

1. Aufgabe

Aufgabe 1 Netz.jpg

a) Aus welchen Formen setzt sich dieses Netz zusammen?
b) Wie heißt der Körper, der sich damit bauen lässt?
c) Wie viele Kanten besitzt dieser Körper?
d) Wie viele Ecken besitzt dieser Körper?
e) Zeichne ein Schrägbild des zum Netzt gehörigen Körpers.

Punkte: 0 / 0



Zeichne drei Schrägbilder des Körpers, dessen Netz hier abgebildet ist, bei denen jedes Mal eine andere Quaderfläche vorne ist.

Netz1234.jpg


 

Texttexttext einfügen 1 texttexttexttexttext einfügen 2 text.




IV. Geometrische Grundbegriffe:  

1. Geometrische Körper - 2. Geraden - 3. Abstände - 4. Parallelogramm - Umfang - 5. Kreise - 6. Winkel - 7. Achsensymmetrie - 8. Netze geometrischer Körper - 9. Schrägbilder
\Rightarrow Weiter zum nächsten Themengebiet
Von „http://rmg.zum.de/index.php?title=P-Seminar/Mathematik_2010-12/IV.9._Schrägbilder&oldid=54274“