VIII.4. Flächeninhalte verschiedener Figuren: Unterschied zwischen den Versionen
K |
|||
| Zeile 2: | Zeile 2: | ||
<imagemap> | <imagemap> | ||
Bild:Erklärbär.PNG|30px|left| | Bild:Erklärbär.PNG|30px|left| | ||
| − | rect 0 0 0 0 [[P-Seminar/Mathematik_2010-12 | + | rect 0 0 0 0 [[P-Seminar/Mathematik_2010-12]] |
| − | default [[P-Seminar/Mathematik_2010-12 | + | default [[P-Seminar/Mathematik_2010-12]] |
desc none | desc none | ||
</imagemap> | </imagemap> | ||
| Zeile 112: | Zeile 112: | ||
<div class="aussen"><div class="menutag">'''VI. Multiplikation und Division ganzer Zahlen'''</div> | <div class="aussen"><div class="menutag">'''VI. Multiplikation und Division ganzer Zahlen'''</div> | ||
| − | *[[P-Seminar/ | + | *[[P-Seminar/Mathematik 2010-12/VI.1. Multiplikation | 1. Multiplikation]] |
| − | *[[P-Seminar/ | + | *[[P-Seminar/Mathematik 2010-12/VI.2 Division | 2. Division]] |
| − | + | ||
</div> | </div> | ||
</div> | </div> | ||
| Zeile 161: | Zeile 161: | ||
<br><br><br><br> | <br><br><br><br> | ||
| + | |||
</div> | </div> | ||
| − | |||
| + | </div> | ||
</div> | </div> | ||
Aktuelle Version vom 23. Oktober 2013, 00:44 Uhr
VIII. Flächen und Flächenmessung:
Erklärung
Flächeninhalt berechnen
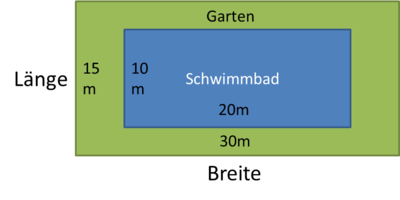
Wenn du eine Fläche hast, zum Beispiel ein Rechteck, und davon den Flächeninhalt bestimmen sollst, dann musst du die Länge der Fläche mit der Breite der Fläche multiplizieren.
Beispiel:
Auf einem 20m x 25m großen begrasten Grundstück befindet sich ein 10m x 20m großes Schwimmbecken.
Wie groß ist der Inhalt der verbleibenden Rasenfläche?
Merke:
Der Flächeninhalt einer Figur lässt sich bestimmen, wenn es möglich ist
(1.) die Figur in Rechtecke zu zerlegen oder
(2.) die geeignet zerlegte Figur zu einem Rechteck neu zusammenzusetzen oder
(3.) die Figur durch Hinzufügen von Rechtecken zu einem Rechteck zu ergänzen.
Aufgaben
Jonas möchte ein Haus bauen. Das Haus soll 18m x 23m groß sein. Es soll sich auf einem Grundstück befinden, das 28m x 30m groß ist. Eine rechteckige Wiese, die 235m lang und 185m breit ist, soll als Baugelände erschlossen werden. Auf Wege, Gräben und dergleichen entfallen 9 875m2. Die einzelnen Bauplätze haben eine Größe von 840m2. Wie viele Bauplätze erhält man? (! 38) (! 43) ( 40) Ein Garten ist 18m lang und ebenso breit; ein anderer 23m lang und 19m breit. Wie groß sind beide Gärten zusammen? ( 761m²) (! 749m²) (! 683m²) Bei einer Flurbereinigung erhält ein Landwirt für seine drei rechteckigen Felder ein neues mit gleicher Bodenqualität. Das erste Feld ist 250 m lang und 100 m breit, das zweite Feld ist 100 m breit und 50 m lang, das dritte Feld ist 0,2 km lang und quadratisch. a) Berechne den Flächeninhalt für jeden der drei Äcker. ( 25000m², 5000m², 40000m²) (! 26000m², 38000m², 4500m²) (! 6000m², 27500m², 39000m²)
Die Fläche eines Rasens beträgt 44m x 37m (das sind 1628m²). Die Fläche eines quadratischen Teichs beträgt 8m x 13m (das sind 104m²).
|
VIII. Flächen und Flächenmessung: