IV.5. Kreise: Unterschied zwischen den Versionen
Aus RMG-Wiki
| Zeile 184: | Zeile 184: | ||
Alle Punkte eines '''Kreises''' haben von seinem '''Mittelpunkt''' den gleichen Abstand.<br /> | Alle Punkte eines '''Kreises''' haben von seinem '''Mittelpunkt''' den gleichen Abstand.<br /> | ||
Dieser Abstand heißt '''Radius''' des Kreises.<br /> | Dieser Abstand heißt '''Radius''' des Kreises.<br /> | ||
| − | Gibt man Mittelpunkt und Radius eines Kreises an, so kann er gezeichnet werden.<br /> | + | Gibt man Mittelpunkt und Radius eines Kreises an, so kann er gezeichnet werden. <br /><br /> |
[[Datei:Mittelpunkt,Radius,Durchmesser.png]] | [[Datei:Mittelpunkt,Radius,Durchmesser.png]] | ||
''' | ''' | ||
| Zeile 196: | Zeile 196: | ||
<div class="multiplechoice-quiz"> | <div class="multiplechoice-quiz"> | ||
| − | + | Welche Oberflächenfigur erhält man, wenn man einen ebenen Schnitt durch eine Kugel macht? | |
| − | (! | + | (! Quadrat) |
| − | ( | + | ( Kugel) |
| − | (! | + | (! Achteck) |
Frage 2 | Frage 2 | ||
Version vom 6. September 2013, 14:02 Uhr
IV. Geometrische Grundbegriffe:
Erklärung
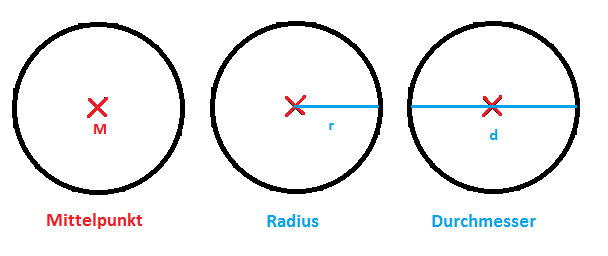
Alle Punkte eines Kreises haben von seinem Mittelpunkt den gleichen Abstand.
Dieser Abstand heißt Radius des Kreises.
Gibt man Mittelpunkt und Radius eines Kreises an, so kann er gezeichnet werden.
Aufgaben
Welche Oberflächenfigur erhält man, wenn man einen ebenen Schnitt durch eine Kugel macht? (! Quadrat) ( Kugel) (! Achteck) Frage 2 (! 1) (! 2) ( 3)
Texttexttext einfügen 1 texttexttexttexttext einfügen 2 text.
|
IV. Geometrische Grundbegriffe:

