V.1. Multiplizieren und Dividieren: Unterschied zwischen den Versionen
| (3 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 184: | Zeile 184: | ||
: Wenn bei einer Summe die einzelnen Summanden den gleichen Wert besitzen | : Wenn bei einer Summe die einzelnen Summanden den gleichen Wert besitzen | ||
: kann man diese als Produkt schreiben | : kann man diese als Produkt schreiben | ||
| − | : z.B 5+5+5=3 | + | : z.B 5+5+5=3<math>\cdot</math>5=15 |
: wobei 3 der 1.Faktor, 5 der 2.Faktor und 15 der Produktwert ist | : wobei 3 der 1.Faktor, 5 der 2.Faktor und 15 der Produktwert ist | ||
| Zeile 202: | Zeile 202: | ||
<div class="multiplechoice-quiz"> | <div class="multiplechoice-quiz"> | ||
| − | Berechne: 5 | + | Berechne: <math>5\cdot8+8+8+8:2+3</math> |
(! 48) | (! 48) | ||
(! 35) | (! 35) | ||
( 63) | ( 63) | ||
| − | Berechne: (6 | + | Berechne: (6<math>\cdot</math>3-3):5-3 |
(0) | (0) | ||
(!-3) | (!-3) | ||
(!3) | (!3) | ||
| − | Berechne: 9 | + | Berechne: 9<math>\cdot</math>45:3<math>\cdot</math>[(9+1-8:2):2] |
(! 945) | (! 945) | ||
(! 135) | (! 135) | ||
( 405) | ( 405) | ||
| − | Berechne: 7 | + | Berechne: 7<math>\cdot</math>3:3<math>\cdot</math>4-7+3<math>\cdot</math>8+4<math>\cdot</math>3-17-8 |
(32) | (32) | ||
(!34) | (!34) | ||
(!42) | (!42) | ||
| − | Berechne:(3 | + | Berechne:(3<math>\cdot</math>5<math>\cdot</math>6-12:2):21 |
(4) | (4) | ||
(!2) | (!2) | ||
(!nicht möglich) | (!nicht möglich) | ||
| − | Berechne: 7 | + | Berechne: 7<math>\cdot</math>3-21<math>\cdot</math>2<math>\cdot</math>(-1):7 |
(27) | (27) | ||
(!0) | (!0) | ||
| Zeile 239: | Zeile 239: | ||
(!15 mal so viel) | (!15 mal so viel) | ||
| − | Berechne:5 | + | Berechne:5<math>\cdot</math>6:10<math>\cdot</math>3<math>\cdot</math>7-1 |
(!63) | (!63) | ||
(62) | (62) | ||
(!64) | (!64) | ||
| − | Berechne:(4-3) | + | Berechne:(4-3)<math>\cdot</math>5-7<math>\cdot</math>8 |
(-51) | (-51) | ||
(!-67) | (!-67) | ||
Aktuelle Version vom 6. Dezember 2013, 15:03 Uhr
V. Multiplikation und Division natürlicher Zahlen:
Erklärung
Multiplikation
- Wenn bei einer Summe die einzelnen Summanden den gleichen Wert besitzen
- kann man diese als Produkt schreiben
- z.B 5+5+5=3
 5=15
5=15
- wobei 3 der 1.Faktor, 5 der 2.Faktor und 15 der Produktwert ist
Division Beispiel: Von 12 ausgehend kann mnan dreimal hintereinander die Zahl 4 abziehen, d.h. die 4 passt dreimal in die 12. Also gilt: 12:4=3
Aufgaben
Berechne: Berechne: (6 Berechne: 9 Berechne: 7 Berechne:(3 Berechne: 7 Berechne: Der Hamburger Sportverein bestreitet dieses Jahr seine 50. Bundesliga Saison, während der FC Augsburg sein 2. Jahr in der höchsten deutschen Liga vertreten ist. Wie viel Jahre mehr spielt der Hsv in der Bundesliga? (25 mal so viel) (!20 mal so viel) (!15 mal so viel) Berechne:5 Berechne:(4-3)
Ein Produkt besteht aus 1. Faktor,2. Faktor und Produktwert und nicht aus Dividend und Divisor.
|
V. Multiplikation und Division natürlicher Zahlen:
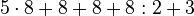 (! 48)
(! 35)
( 63)
(! 48)
(! 35)
( 63)

