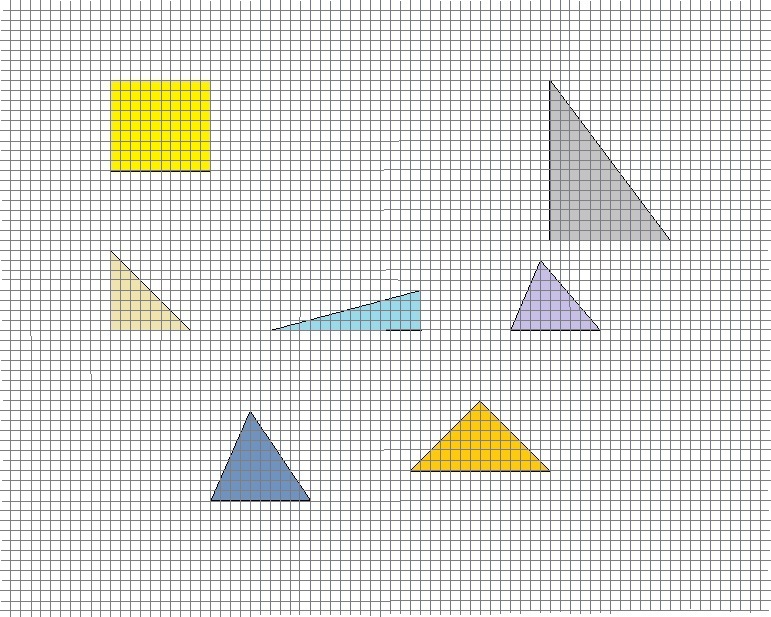VIII.1. Flächeninhalte vergleichen und messen: Unterschied zwischen den Versionen
| (9 dazwischenliegende Versionen von 5 Benutzern werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
<imagemap> | <imagemap> | ||
Bild:Erklärbär.PNG|30px|left| | Bild:Erklärbär.PNG|30px|left| | ||
| − | rect 0 0 0 0 [[ | + | rect 0 0 0 0 [[P-Seminar/Mathematik_2010-12]] |
| − | default [[ | + | default [[P-Seminar/Mathematik_2010-12]] |
desc none | desc none | ||
</imagemap> | </imagemap> | ||
| − | + | <div class="aussen"><div class="menutag">[[P-Seminar/Mathematik_2010-12|Hauptmenü]]</div> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | <div class="aussen"><div class="menutag">[[P-Seminar/Mathematik_2010-12| | + | |
;----------------------------------------------------------------------------------- | ;----------------------------------------------------------------------------------- | ||
| − | <popup name=" | + | <popup name="I.Natürliche Zahlen "> |
<div class="menuebox"><div class="menue"> | <div class="menuebox"><div class="menue"> | ||
| Zeile 120: | Zeile 112: | ||
<div class="aussen"><div class="menutag">'''VI. Multiplikation und Division ganzer Zahlen'''</div> | <div class="aussen"><div class="menutag">'''VI. Multiplikation und Division ganzer Zahlen'''</div> | ||
| − | *[[P-Seminar/ | + | *[[P-Seminar/Mathematik 2010-12/VI.1. Multiplikation | 1. Multiplikation]] |
| − | *[[P-Seminar/ | + | *[[P-Seminar/Mathematik 2010-12/VI.2 Division | 2. Division]] |
| − | + | ||
</div> | </div> | ||
</div> | </div> | ||
| Zeile 168: | Zeile 160: | ||
<br><br><br><br> | <br><br><br><br> | ||
| + | |||
</div> | </div> | ||
| Zeile 175: | Zeile 168: | ||
</div> | </div> | ||
| − | |||
<br> | <br> | ||
| Zeile 191: | Zeile 183: | ||
<br /> | <br /> | ||
| − | [[Datei: | + | [[Datei:quadrate-mit-dreiecken.jpg]] |
<br><br><br> | <br><br><br> | ||
| − | In der oberen Abbildung seht ihr zwei Quadrate. Jedes dieser Quadrate besteht aus einer Anzahl gleich großer Dreiecke. Wie ihr sehen könnt ist die Anzahl im | + | In der oberen Abbildung seht ihr zwei Quadrate. Jedes dieser Quadrate besteht aus einer Anzahl gleich großer Dreiecke. Wie ihr sehen könnt ist die Anzahl im roten Quadrat deutlich größer. Das liegt daran, dass das rote Quadrat aus mehr Dreiecken besteht als das blaue. |
| − | Im | + | Im blauen sind zwei Dreiecke zu sehen, während es im roten vier sind. |
Durch Kästchenzählen fällt es im Matheunterricht beispielsweise viel leichter einzuschätzen, welche abgebildete Figur am größten ist bzw. wie groß jede Figur überhaupt ist. | Durch Kästchenzählen fällt es im Matheunterricht beispielsweise viel leichter einzuschätzen, welche abgebildete Figur am größten ist bzw. wie groß jede Figur überhaupt ist. | ||
| Zeile 204: | Zeile 196: | ||
<br> | <br> | ||
[[Datei:Kästchen1.gif]] | [[Datei:Kästchen1.gif]] | ||
| − | + | <br> | |
| + | <br> | ||
In diesem Beispiel seht ihr ein Rechteck. Durch Kästchenzählen könnt ihr herausfinden, wie groß (in Kästchen) die Abbildung ist. | In diesem Beispiel seht ihr ein Rechteck. Durch Kästchenzählen könnt ihr herausfinden, wie groß (in Kästchen) die Abbildung ist. | ||
| − | Diese Abbildung hat eine Breite von 7Kästchen und eine Länge von 9Kästchen. Wenn ihr diese beiden Zahlen miteinander multipliziert erhaltet ihr die Größe des Rechtecks, nämlich 63Kästchen. | + | Diese Abbildung hat eine Breite von <span style="color: red">7Kästchen</span> und eine Länge von <span style="color: red">9Kästchen</span>. Wenn ihr diese beiden Zahlen miteinander multipliziert erhaltet ihr die Größe des Rechtecks, nämlich <span style="color: red">63Kästchen</span>. |
| − | (Ihr könnt jetzt auch noch ermitteln, wie groß die Figur in cm ist. Das könnt ihr leicht herausfinden, denn ein Kästchen entspricht üblicherweise 0,5cm. Also ist die Breite des Rechtecks 3,5cm und die Länge 4,5cm. Somit hat es eine Gesamtgröße von 31,5cm.) | + | (Ihr könnt jetzt auch noch ermitteln, wie groß die Figur in cm ist. Das könnt ihr leicht herausfinden, denn ein Kästchen entspricht üblicherweise 0,5cm. Also ist die Breite des Rechtecks <span style="color: blue">3,5cm</span> und die Länge <span style="color: blue">4,5cm</span>. Somit hat es eine Gesamtgröße von <span style="color: blue">31,5cm</span>.) |
''' | ''' | ||
</div> | </div> | ||
| Zeile 218: | Zeile 211: | ||
<div class="multiplechoice-quiz"> | <div class="multiplechoice-quiz"> | ||
| − | + | Welche Dreiecke haben einen größeren Flächeninhalt als das gelbe Viereck? | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | [[Datei:Seminar.jpg]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | |||
| − | + | (! gelbes Dreieck) | |
| − | + | (! dunkelblaues Dreieck) | |
| − | + | (! Gelbes Dreieck) | |
| + | (! hellblaues Dreieck) | ||
| + | (! braunes Dreieck) | ||
| + | (! hell lilanes Dreieck) | ||
| + | ( Lilanes Dreieck) | ||
| + | </div> | ||
| + | |||
Aktuelle Version vom 21. November 2013, 06:16 Uhr
VIII. Flächen und Flächenmessung:
Erklärung
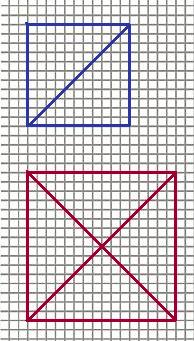
In der oberen Abbildung seht ihr zwei Quadrate. Jedes dieser Quadrate besteht aus einer Anzahl gleich großer Dreiecke. Wie ihr sehen könnt ist die Anzahl im roten Quadrat deutlich größer. Das liegt daran, dass das rote Quadrat aus mehr Dreiecken besteht als das blaue.
Im blauen sind zwei Dreiecke zu sehen, während es im roten vier sind.
Durch Kästchenzählen fällt es im Matheunterricht beispielsweise viel leichter einzuschätzen, welche abgebildete Figur am größten ist bzw. wie groß jede Figur überhaupt ist.
Beispiel:
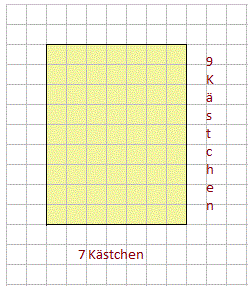
In diesem Beispiel seht ihr ein Rechteck. Durch Kästchenzählen könnt ihr herausfinden, wie groß (in Kästchen) die Abbildung ist.
Diese Abbildung hat eine Breite von 7Kästchen und eine Länge von 9Kästchen. Wenn ihr diese beiden Zahlen miteinander multipliziert erhaltet ihr die Größe des Rechtecks, nämlich 63Kästchen.
(Ihr könnt jetzt auch noch ermitteln, wie groß die Figur in cm ist. Das könnt ihr leicht herausfinden, denn ein Kästchen entspricht üblicherweise 0,5cm. Also ist die Breite des Rechtecks 3,5cm und die Länge 4,5cm. Somit hat es eine Gesamtgröße von 31,5cm.)
Aufgaben
Welche Dreiecke haben einen größeren Flächeninhalt als das gelbe Viereck?
(! gelbes Dreieck) (! dunkelblaues Dreieck) (! Gelbes Dreieck) (! hellblaues Dreieck) (! braunes Dreieck) (! hell lilanes Dreieck) ( Lilanes Dreieck)
|
VIII. Flächen und Flächenmessung: