IV.4. Parallelogramme - Umfang: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
 
(16 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt)
Zeile 2: Zeile 2:
 
<imagemap>
 
<imagemap>
 
Bild:Erklärbär.PNG‎|30px|left|
 
Bild:Erklärbär.PNG‎|30px|left|
−
rect 0 0 0 0 [[Benutzer:Thamm_Pascal]]
+
rect 0 0 0 0 [[P-Seminar/Mathematik_2010-12]]
−
default [[Benutzer:Thamm_Pascal]]
+
default [[P-Seminar/Mathematik_2010-12]]
 
desc none
 
desc none
 
</imagemap>
 
</imagemap>
  
−
<div class="aussen"><div class="menutag">'''IV. Geometrische Grundbegriffe'''</div>
+
<div class="aussen"><div class="menutag">[[P-Seminar/Mathematik_2010-12|Hauptmenü]]</div>
−
*[[P-Seminar/Mathematik_2010-12/IV.1._Geometrische_Körper|1. Geometrische Körper]]
+
−
*[[P-Seminar/Mathematik_2010-12/IV.2._Geraden|2. Geraden]]
+
−
*[[P-Seminar/Mathematik_2010-12/IV.3._Abstände|3. Abstände]]
+
−
*[[P-Seminar/Mathematik_2010-12/IV.4._Parallelogramme_-_Umfang|4. Parallelogramme - Umfang]]
+
−
*[[P-Seminar/Mathematik_2010-12/IV.5._Kreise|5. Kreise]]
+
−
*[[P-Seminar/Mathematik_2010-12/IV.6._Winkel|6. Winkel]]
+
−
*[[P-Seminar/Mathematik_2010-12/IV.7._Achsensymmetrie|7. Achsensymmetrie]]
+
−
*[[P-Seminar/Mathematik_2010-12/IV.8._Netze_geometrischer_Körper|8. Netze geometrischer Körper]]
+
−
*[[P-Seminar/Mathematik_2010-12/IV.9._Schrägbilder|9. Schrägbilder]]
+
−
</div>
+
−
 
+
−
<div class="aussen"><div class="menutag">[[P-Seminar/Mathematik_2010-12|5.Klasse Mathe]]</div>
+
 
;-----------------------------------------------------------------------------------
 
;-----------------------------------------------------------------------------------
−
<popup name="1.Natürliche Zahlen ">
+
<popup name="I.Natürliche Zahlen ">
  
 
<div class="menuebox"><div class="menue">
 
<div class="menuebox"><div class="menue">
Zeile 124: Zeile 112:
  
 
<div class="aussen"><div class="menutag">'''VI. Multiplikation und Division ganzer Zahlen'''</div>
 
<div class="aussen"><div class="menutag">'''VI. Multiplikation und Division ganzer Zahlen'''</div>
−
*[[P-Seminar/Mathematik_2010-12/VI.1._Multiplizieren|1. Multiplizieren]]
+
*[[P-Seminar/Mathematik 2010-12/VI.1. Multiplikation | 1. Multiplikation]]
−
*[[P-Seminar/Mathematik_2010-12/VI.2._Dividieren|2. Dividieren]]
+
*[[P-Seminar/Mathematik 2010-12/VI.2 Division | 2. Division]]
−
*[[P-Seminar/Mathematik_2010-12/VI.3._Rechengesetze_und_Rechenvorteile|3. Rechengesetze und Rechenvorteile]]
+
 
 
</div>
 
</div>
 
</div>
 
</div>
Zeile 172: Zeile 160:
  
 
<br><br><br><br>
 
<br><br><br><br>
 +
 
                        
 
                        
 
</div>
 
</div>
Zeile 178: Zeile 167:
 
</div>
 
</div>
 
</div>
 
</div>
−
 
 
<br>
 
<br>
 
<br>
 
<br>
Zeile 186: Zeile 174:
 
''IV. Geometrische Grundbegriffe:'' &nbsp;  
 
''IV. Geometrische Grundbegriffe:'' &nbsp;  
 
<br />
 
<br />
−
[[P-Seminar/Mathematik 2010-12/IV.1. Geometrische Körper | 1. Geometrische Körper ]] - [[P-Seminar/Mathematik 2010-12/IV.2. Geraden | 2. Geraden ]] - [[P-Seminar/Mathematik 2010-12/IV.3. Abstände| 3. Abstände]] - [[P-Seminar/Mathematik 2010-12/IV.4. Parallelogramme - Umfang | 4. Parallelogramm - Umfang]] - [[P-Seminar/Mathematik 2010-12/IV.5. Kreise | 5. Kreise]] - [[P-Seminar/Mathematik 2010-12/IV.6. Winkel | 6. Winkel]] - [[P-Seminar/Mathematik 2010-12/IV.7. Achsensymmetrie | 7. Achsensymmetrie]] - [[P-Seminar/Mathematik 2010-12/IV.8. Netze geometrischer Körper | 8. Netze geometrischer Körper]] - [[P-Seminar/Mathematik 2010-12/IV.9. Schrägbilder | 9. Schrägbilder]]</div>
+
[[P-Seminar/Mathematik 2010-12/IV.1. Geometrische Körper | 1. Geometrische Körper ]] - [[P-Seminar/Mathematik 2010-12/IV.2. Geraden | 2. Geraden]] - [[P-Seminar/Mathematik 2010-12/IV.3. Abstände| 3. Abstände]] - [[P-Seminar/Mathematik 2010-12/IV.4. Parallelogramme - Umfang | 4. Parallelogramm - Umfang]] - [[P-Seminar/Mathematik 2010-12/IV.5. Kreise | 5. Kreise]] - [[P-Seminar/Mathematik 2010-12/IV.6. Winkel | 6. Winkel]] - [[P-Seminar/Mathematik 2010-12/IV.7. Achsensymmetrie | 7. Achsensymmetrie]] - [[P-Seminar/Mathematik 2010-12/IV.8. Netze geometrischer Körper | 8. Netze geometrischer Körper]] - [[P-Seminar/Mathematik 2010-12/IV.9. Schrägbilder | 9. Schrägbilder]]</div>
  
 
<br />
 
<br />
Zeile 199: Zeile 187:
 
''Umfang'': "Der '''Umfang''' einer Figur ist die Länge ihrer Randlinien."<br />
 
''Umfang'': "Der '''Umfang''' einer Figur ist die Länge ihrer Randlinien."<br />
 
Ein Parallelogramm mit den Seitenlängen a und b hat den Umfang U:<br />
 
Ein Parallelogramm mit den Seitenlängen a und b hat den Umfang U:<br />
−
U = a+a+b+b<br />
+
U = <span style="orange: color">a</span>+<span style="orange: color">a</span>+<span style="blue: color">b</span>+<span style="blue: color">b</span><br />
−
U = 2a + 2b<br />
+
U = 2<span style="color: black">a</span> + 2<span style="green: color">b</span><br />
−
U = 2(a+b)<br />
+
U = 2(<span style="dark orange: color">a</span>+<span style="green: color">b</span>)<br />
 
'''
 
'''
 +
[[Datei:Parallelogramm.jpg]]
 
</div>
 
</div>
  
Zeile 225: Zeile 214:
 
8. a=29cm, b=12cm: { 82m }
 
8. a=29cm, b=12cm: { 82m }
 
9. a=31m, b=56m: { 174m }
 
9. a=31m, b=56m: { 174m }
−
</quiz>
+
 
−
<br />
+
{'''Ein rechteckiges Grundstück hat eine Länge von 120m und eine Breite von 40m. Wie groß ist der Umfang?'''
−
<quiz display="simple">
+
−
{Ein rechteckiges Grundstück hat eine Länge von 120m und eine Breite von 40m. Wie groß ist der Umfang?
+
 
| type="{}"}
 
| type="{}"}
 
{ 340m }
 
{ 340m }
−
</quiz>
+
 
−
<quiz display="simple">
+
{'''Wie groß ist der Umfang wenn die Länge 80m und die Breite 15m sind?'''
−
{Wie groß ist der Umfang wenn die Länge 80m und die Breite 15m sind?
+
 
| type="{}"}
 
| type="{}"}
 
{ 190m }
 
{ 190m }
 
</quiz>
 
</quiz>
−
'''2.''' Ordne die Rechtecke nach der Größe ihres Umfangs. Beginne mit dem kleinsten Umfang.
+
'''4. Ordne die Rechtecke nach der Größe ihres Umfangs. Beginne mit dem kleinsten Umfang. Klicke auf die Rechtecke um deren richtige Größe zu erkennen.'''
 
<iframe src="http://LearningApps.org/show?app=60685" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>
 
<iframe src="http://LearningApps.org/show?app=60685" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>
 
<br />
 
<br />
−
Frage 1
+
'''5.Welchen Umfang besitzt das Parallelogramm mit...'''
−
(! A)
+
<br />
−
( B)
+
−
(! C)
+
  
−
Frage 2
+
...Breite: 21cm , Länge: 29cm
−
(! 1)
+
(! 87)
−
(! 2)
+
( 100)
−
( 3)
+
(! 54)
 +
 
 +
<br />
 +
...Breite: 45m , Länge: 4m
 +
( 98)
 +
(! 99)
 +
(! 97)
  
 
</div>
 
</div>
Zeile 254: Zeile 244:
  
 
&nbsp;
 
&nbsp;
 +
'''6.Vervollständige den Satz.'''
 
<div class="lueckentext-quiz">
 
<div class="lueckentext-quiz">
−
Texttexttext <strong>einfügen 1</strong> texttexttexttexttext <strong>einfügen 2</strong> text.</div>
+
Der <strong>Umfang</strong> einer <strong>Figur</strong> ist die <strong>Länge</strong> ihrer <strong>Randlinien</strong> .</div>
  
  

Aktuelle Version vom 2. Dezember 2013, 14:57 Uhr

Erklärbär.PNGP-Seminar/Mathematik 2010-12
Hauptmenü
-----------------------------------------------------------------------------------
















 

IV. Geometrische Grundbegriffe:  

1. Geometrische Körper - 2. Geraden - 3. Abstände - 4. Parallelogramm - Umfang - 5. Kreise - 6. Winkel - 7. Achsensymmetrie - 8. Netze geometrischer Körper - 9. Schrägbilder


Erklärung

"Vierecke, bei denen gegenüberliegende Seiten parallel sind heißen Parallelogramme."
Jedes Quadrat, Rechteck und jede Raute sind Parallelogramme.

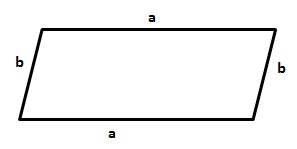
Umfang: "Der Umfang einer Figur ist die Länge ihrer Randlinien."
Ein Parallelogramm mit den Seitenlängen a und b hat den Umfang U:
U = a+a+b+b
U = 2a + 2b
U = 2(a+b)
Parallelogramm.jpg


  Aufgaben

1. Berechne den Umfang

1. a=5cm, b=3cm:
2. a=10m, b=2m:
3. a=15mm, b=7mm:
4. a=6cm, b=9cm:
5. a=23cm, b=2cm:
6. a=6m, b=10m:
7. a=3mm, b=3mm:
8. a=29cm, b=12cm:
9. a=31m, b=56m:

2. Ein rechteckiges Grundstück hat eine Länge von 120m und eine Breite von 40m. Wie groß ist der Umfang?


3. Wie groß ist der Umfang wenn die Länge 80m und die Breite 15m sind?


Punkte: 0 / 0

4. Ordne die Rechtecke nach der Größe ihres Umfangs. Beginne mit dem kleinsten Umfang. Klicke auf die Rechtecke um deren richtige Größe zu erkennen. [ LearningApps.org is not an authorized iframe site ]
5.Welchen Umfang besitzt das Parallelogramm mit...

...Breite: 21cm , Länge: 29cm (! 87) ( 100) (! 54)


...Breite: 45m , Länge: 4m ( 98) (! 99) (! 97)


  6.Vervollständige den Satz.

Der Umfang einer Figur ist die Länge ihrer Randlinien .




IV. Geometrische Grundbegriffe:  

1. Geometrische Körper - 2. Geraden - 3. Abstände - 4. Parallelogramm - Umfang - 5. Kreise - 6. Winkel - 7. Achsensymmetrie - 8. Netze geometrischer Körper - 9. Schrägbilder
Von „http://rmg.zum.de/index.php?title=P-Seminar/Mathematik_2010-12/IV.4._Parallelogramme_-_Umfang&oldid=55267“