IV.9. Schrägbilder: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
 
(34 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
 +
<div class="menuebox"><div class="menue">
 +
<imagemap>
 +
Bild:Erklärbär.PNG‎|30px|left|
 +
rect 0 0 0 0 [[P-Seminar/Mathematik_2010-12]]
 +
default [[P-Seminar/Mathematik_2010-12]]
 +
desc none
 +
</imagemap>
 +
 +
<div class="aussen"><div class="menutag">[[P-Seminar/Mathematik_2010-12|Hauptmenü]]</div>
 +
;-----------------------------------------------------------------------------------
 +
<popup name="I.Natürliche Zahlen ">
 +
 +
<div class="menuebox"><div class="menue">
 +
 +
<div class="aussen"><div class="menutag">'''I.Natürliche Zahlen'''</div>
 +
*[[P-Seminar/Mathematik_2010-12/I.1._Zählen_und_Ordnen|Zählen und Ordnen]]
 +
*[[P-Seminar/Mathematik_2010-12/I.2._Veranschaulichung_von_Zahlen|Veranschaulichung von Zahlen]]
 +
*[[P-Seminar/Mathematik_2010-12/I.3._Das_Dezimalsystem|Das Dezimalsystem]]
 +
*[[P-Seminar/Mathematik_2010-12/I.4._Römische_Zahlen|Römische Zahlen]]
 +
*[[P-Seminar/Mathematik_2010-12/I.5._Zahlenmengen|Zahlenmengen]]
 +
*[[P-Seminar/Mathematik_2010-12/I.6._Runden|Runden]]
 +
</div>
 +
</div>
 +
</div>
 +
 +
</popup>
 +
 +
 +
 +
<popup name="II. Addition und Subtraktion natürlicher Zahlen ">
 +
 +
<div class="menuebox"><div class="menue">
 +
 +
<div class="aussen"><div class="menutag">'''II. Addition und Subtraktion natürlicher Zahlen'''</div>
 +
*[[P-Seminar/Mathematik_2010-12/II.1._Addieren_und_Subtrahieren|1.Addieren und Subtrahieren]]
 +
*[[P-Seminar/Mathematik_2010-12/II.2._Rechengesetze_und_Rechenvorteile|2.Rechengesetze und Rechenvorteile]]
 +
*[[P-Seminar/Mathematik_2010-12/II.3._Terme|3.Terme]]
 +
</div>
 +
</div>
 +
</div>
 +
 +
</popup>
 +
 +
 +
 +
<popup name="III. Die ganzen Zahlen; Addition und Subtraktion ">
 +
 +
<div class="menuebox"><div class="menue">
 +
 +
<div class="aussen"><div class="menutag">'''III. Die ganzen Zahlen; Addition und Subtraktion'''</div>
 +
*[[P-Seminar/Mathematik_2010-12/III.1._Negative_Zahlen|1.Negative Zahlen]]
 +
*[[P-Seminar/Mathematik_2010-12/III.2._Vorzeichenschreibweise|2.Vorzeichenschreibweise]]
 +
*[[P-Seminar/Mathematik_2010-12/III.3._Anordnung_und_Betrag|3.Anordnung und Betrag]]
 +
*[[P-Seminar/Mathematik_2010-12/III.4._Addieren|4.Addieren]]
 +
*[[P-Seminar/Mathematik_2010-12/III.5._Subtrahieren|5.Subtrahieren]]
 +
*[[P-Seminar/Mathematik_2010-12/III.6._Rechnen_mit_Summen_und_Differenzen|6.Rechnen mit Summen und Differenzen]]
 +
</div>
 +
</div>
 +
</div>
 +
 +
</popup>
 +
 +
 +
 +
<popup name="IV. Geometrische Grundbegriffe ">
 +
 +
<div class="menuebox"><div class="menue">
 +
 +
<div class="aussen"><div class="menutag">'''IV. Geometrische Grundbegriffe'''</div>
 +
*[[P-Seminar/Mathematik_2010-12/IV.1._Geometrische_Körper|1. Geometrische Körper]]
 +
*[[P-Seminar/Mathematik_2010-12/IV.2._Geraden|2. Geraden]]
 +
*[[P-Seminar/Mathematik_2010-12/IV.3._Abstände|3. Abstände]]
 +
*[[P-Seminar/Mathematik_2010-12/IV.4._Parallelogramme_-_Umfang|4. Parallelogramme - Umfang]]
 +
*[[P-Seminar/Mathematik_2010-12/IV.5._Kreise|5. Kreise]]
 +
*[[P-Seminar/Mathematik_2010-12/IV.6._Winkel|6. Winkel]]
 +
*[[P-Seminar/Mathematik_2010-12/IV.7._Achsensymmetrie|7. Achsensymmetrie]]
 +
*[[P-Seminar/Mathematik_2010-12/IV.8._Netze_geometrischer_Körper|8. Netze geometrischer Körper]]
 +
*[[P-Seminar/Mathematik_2010-12/IV.9._Schrägbilder|9. Schrägbilder]]
 +
</div>
 +
</div>
 +
</div>
 +
 +
</popup>
 +
 +
 +
 +
<popup name="V. Multiplikation und Division natürlicher Zahlen ">
 +
 +
<div class="menuebox"><div class="menue">
 +
 +
<div class="aussen"><div class="menutag">'''V. Multiplikation und Division natürlicher Zahlen'''</div>
 +
*[[P-Seminar/Mathematik_2010-12/V.1._Multiplizieren_und_Dividieren|1. Multiplizieren und Dividieren]]
 +
*[[P-Seminar/Mathematik_2010-12/V.2._Rechnen_mit_Null_und_Eins|2. Rechnen mit Null und Eins]]
 +
*[[P-Seminar/Mathematik_2010-12/V.3._Schriftliches_Multiplizieren_und_Dividieren|3. Schriftliches Multiplizieren und Dividieren]]
 +
*[[P-Seminar/Mathematik_2010-12/V.4._Verbindung_der_Grundrechenarten|4. Verbindung der Grundrechenarten]]
 +
*[[P-Seminar/Mathematik_2010-12/V.5._Rechengesetze_und_Rechenvorteile|5. Rechengesetze und Rechenvorteile]]
 +
*[[P-Seminar/Mathematik_2010-12/V.6._Potenzieren|6. Potenzieren]]
 +
*[[P-Seminar/Mathematik_2010-12/V.7._Faktorisieren_von_Zahlen|7. Faktorisieren von Zahlen]]
 +
*[[P-Seminar/Mathematik_2010-12/V.8._Terme|8. Terme]]
 +
*[[P-Seminar/Mathematik_2010-12/V.9._Abzählen_am_Baumdiagramm|9. Abzählen am Baumdiagramm]]
 +
</div>
 +
</div>
 +
</div>
 +
 +
</popup>
 +
 +
 +
 +
<popup name="VI. Multiplikation und Division ganzer Zahlen ">
 +
 +
<div class="menuebox"><div class="menue">
 +
 +
<div class="aussen"><div class="menutag">'''VI. Multiplikation und Division ganzer Zahlen'''</div>
 +
*[[P-Seminar/Mathematik 2010-12/VI.1. Multiplikation | 1. Multiplikation]]
 +
*[[P-Seminar/Mathematik 2010-12/VI.2 Division | 2. Division]]
 +
 +
</div>
 +
</div>
 +
</div>
 +
 +
</popup>
 +
 +
 +
 +
<popup name="VII. Größen und ihre Einheiten ">
 +
 +
<div class="menuebox"><div class="menue">
 +
 +
<div class="aussen"><div class="menutag">'''VII. Größen und ihre Einheiten'''</div>
 +
*[[P-Seminar/Mathematik_2010-12/VII.1._Messen|1. Messen]]
 +
*[[P-Seminar/Mathematik_2010-12/VII.2._Längen|2. Längen]]
 +
*[[P-Seminar/Mathematik_2010-12/VII.3._Rechnen_mit_Größen|3. Rechnen mit Größen]]
 +
*[[P-Seminar/Mathematik_2010-12/VII.4._Maßstab|4. Maßstab]]
 +
*[[P-Seminar/Mathematik_2010-12/VII.5._Massen|5. Massen]]
 +
*[[P-Seminar/Mathematik_2010-12/VII.6._Geld|6. Geld]]
 +
*[[P-Seminar/Mathematik_2010-12/VII.7._Zeit|7. Zeit]]
 +
</div>
 +
</div>
 +
</div>
 +
 +
</popup>
 +
 +
 +
 +
<popup name="VIII. Flächen und Flächenmessung ">
 +
 +
<div class="menuebox"><div class="menue">
 +
 +
<div class="aussen"><div class="menutag">'''VIII. Flächen und Flächenmessung'''</div>
 +
*[[P-Seminar/Mathematik_2010-12/VIII.1._Flächeninhalte_vergleichen_und_messen|1. Flächeninhalte vergleichen und messen]]
 +
*[[P-Seminar/Mathematik_2010-12/VIII.2._Flächeneinheiten|2. Flächeneinheiten]]
 +
*[[P-Seminar/Mathematik_2010-12/VIII.3._Flächeninhalt_des_Rechtecks|3. Flächeninhalt des Rechtecks]]
 +
*[[P-Seminar/Mathematik_2010-12/VIII.4._Flächeninhalte_verschiedener_Figuren|4. Flächeninhalte verschiedener Figuren]]
 +
*[[P-Seminar/Mathematik_2010-12/VIII.5._Oberflächeninhalt_des_Quaders|5. Oberflächeninhalt des Quaders]]
 +
</div>
 +
</div>
 +
</div>
 +
 +
</popup>
 +
 +
<br><br><br><br>
 +
 +
                     
 +
</div>
 +
 +
 +
</div>
 +
</div>
 +
<br>
 +
<br>
 +
 
<div style="font: 10pt Comic Sans MS; padding:5px; border-bottom:1px solid #AAAAAA;">&nbsp;
 
<div style="font: 10pt Comic Sans MS; padding:5px; border-bottom:1px solid #AAAAAA;">&nbsp;
 
<div style="margin:0; margin-right:4px; margin-left:0px; border:1px solid  #6C7B8B; padding: 0em 0em 0em 1em; background-color:#FFB90F;">
 
<div style="margin:0; margin-right:4px; margin-left:0px; border:1px solid  #6C7B8B; padding: 0em 0em 0em 1em; background-color:#FFB90F;">
 
''IV. Geometrische Grundbegriffe:'' &nbsp;  
 
''IV. Geometrische Grundbegriffe:'' &nbsp;  
 
<br />
 
<br />
−
[[P-Seminar/Mathematik 2010-12/IV.1. Geometrische Körper | 1. Geometrische Körper ]] - [[P-Seminar/Mathematik 2010-12/IV.2. Geraden | 2. Geraden ]] - [[P-Seminar/Mathematik 2010-12/IV.3. Abstände| 3. Abstände]] - [[P-Seminar/Mathematik 2010-12/IV.4. Parallelogramme - Umfang | 4. Parallelogramm - Umfang]] - [[P-Seminar/Mathematik 2010-12/IV.5. Kreise | 5. Kreise]] - [[P-Seminar/Mathematik 2010-12/IV.6. Winkel | 6. Winkel]] - [[P-Seminar/Mathematik 2010-12/IV.7. Achsensymmetrie | 7. Achsensymmetrie]] - [[P-Seminar/Mathematik 2010-12/IV.8. Netze geometrischer Körper | 8. Netze geometrischer Körper]] - [[P-Seminar/Mathematik 2010-12/IV.9. Schrägbilder | 9. Schrägbilder]]</div>
+
[[P-Seminar/Mathematik 2010-12/IV.1. Geometrische Körper | 1. Geometrische Körper ]] - [[P-Seminar/Mathematik 2010-12/IV.2. Geraden | 2. Geraden]] - [[P-Seminar/Mathematik 2010-12/IV.3. Abstände| 3. Abstände]] - [[P-Seminar/Mathematik 2010-12/IV.4. Parallelogramme - Umfang | 4. Parallelogramm - Umfang]] - [[P-Seminar/Mathematik 2010-12/IV.5. Kreise | 5. Kreise]] - [[P-Seminar/Mathematik 2010-12/IV.6. Winkel | 6. Winkel]] - [[P-Seminar/Mathematik 2010-12/IV.7. Achsensymmetrie | 7. Achsensymmetrie]] - [[P-Seminar/Mathematik 2010-12/IV.8. Netze geometrischer Körper | 8. Netze geometrischer Körper]] - [[P-Seminar/Mathematik 2010-12/IV.9. Schrägbilder | 9. Schrägbilder]]</div>
  
 
<br />
 
<br />
Zeile 14: Zeile 185:
 
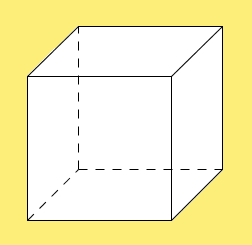
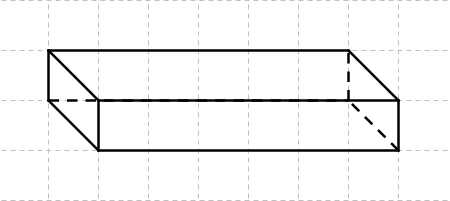
: Als Schrägbild bezeichnet man einen Körper, der auf einer ebenen Fläche (z.B.einem Blatt Papier) aus schräger Perspektive 3-dimensional dargestellt wird.
 
: Als Schrägbild bezeichnet man einen Körper, der auf einer ebenen Fläche (z.B.einem Blatt Papier) aus schräger Perspektive 3-dimensional dargestellt wird.
  
 +
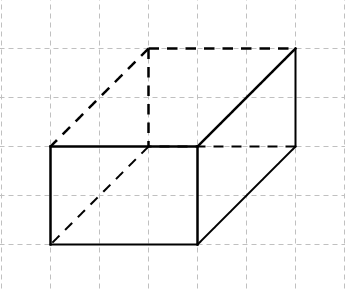
[[Datei:Schrägbild Würfel.jpg]]
 +
<br/>
 +
:: Schrägbild eines Würfels
  
−
:: <ggb_applet width="190" height="203"  version="4.0" ggbBase64="UEsDBBQACAgIAHB5jEIAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIAHB5jEIAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Vrbbts4EH1uv2Kg59oWdXdht2jSpg2Qtguku1jsGyXRMmNZ0oryrejH75CUZDtKutV2EbgG4vA2nOGcM8OLk8nr7TKFNSsFz7OpQYamASyL8phnydRYVbNBYLx+9XySsDxhYUlhlpdLWk0NR0ryeGqw0I/j2GIDYrvmwLG8YBBafjAwvXBmubOIRUFoAGwFf5nln+iSiYJG7DaasyW9ySNaKcPzqipejkabzWbYmBrmZTJKknC4FbEBuMxMTI268hLVHU3a2ErcMk0y+vPjjVY/4JmoaBYxA6QLK/7q+bPJhmdxvoENj6v51LBMz4A548kcfbLJ2ICRFCoQkIJFFV8zgVMPmsrnalkYSoxmcvyZrkHaumNAzNc8ZuXUMIdj3wx82w88x/R9zzcgLznLqlqU1CZHjbLJmrON1ipryqBjQJXnaUilQvj2DSzTMuGFLIguLCw8Tw+Zus+0dWHpwtGFq2UcPd3Roo6WcbSMYxuw5oKHKZsaM5oKBJBnsxLJa9ui2qVMrafu2DtPXqBPgn9FYdvEKNGIY79pvpAfDz+OHBgdO0kOrFblqqfRxiQZ9zBp/ZSjdmPTeshNy33ETe87RrXfP+Sne2ATTakf9elYtL/n5n2Luv1zBj3nSVycjJpUmdTZAWIuZevoqdhSyHyxx+COZdgTcDE3PB+j3AUyxsK3ALMBiAuOi00SgCdLH2wfBxywIQApR2xQyeEG+MvxlTIPXFQme33MSSBoyAHXBqJyygHMJFB5iTlq2SjhuuDiJGmeWFKF7YHjYcsOwME1ypT0CQraOBHbaN4Cm4AtJxMfLA88qY84MtW9QC4dVVrgmeARqRCzGjNaZzPKB2BLb7waLp4Vq6qGqEY9WsYNXFVetN0ojhvSftfTG9TRpvhsktKQpXhO3EoqAdY0ldwpS7M8q6BNDt2XlLSY80jcsqrCWQLu6Jre0Iptr1BaNLaVbJRn4rcyry7zdLXMBECUp2azUKyTg7q1dyZP7YMB53DAPRjwDur+g3ZzHIGVYGg/L0UjTuP4Wkrs9waE8nOW7i5KRhdFzo/dmIzUkTNhqyjlMafZHxit0orEBZoTSO1XzQlEfLdZSF7GtzuBIQzbv1iZYwKQoevYvjceW64TWCgJOz1iEXPo26bvuYEf2JaPp5iIqMw9ezwcu5bvOfgJxq6DqbWrhxxziGdCYHmeQ7yxpc2ydcsO3bK9o0nJ2ziR9WtxkadxO6xcv6RFtSrVvQE3xlI69CZLUqbCQ221eChHizDf3urstrWuL7sCW3WQhImCHHBfsFz0MKnLUJdKRq6slTKVjKkk2kDjcTtO0DUpocpQl0oKI1cvrfaUNF4SszHDhdrNTOM4Z1TcT42tAauMVze6hfnDo0XtK9EzPq2WIWvD51gpeVhpf52T0b34mixYmbG0Dmckc5WvhM7Og0iPWcSX2NQDjcuSr99xAbo3ZknJmoWn6lKmETucoyO1061UXZX58jpbf8FguLeAyahZ5UREJS9kzEGIZ8CC7cMq5oLiERIfzpP5h65H8qhAeCoJDWbmqprnpbp34YaCpUy7lC3xmgWVii8Voi3Mb9T1TeIJeXiHe9p9HvaM4fiDwabCkqbFnMo7Xu11SnesPMJB6fuYx/fRQfCVC5jhhSa3YEzHhV4wVgpUp/LpaIdCuAVsp8ZAXdZ39aX9qy717VX6KpNM23QOe+8RhdGjYfoXwC7OCTDnCQC7PAPArCfE6+0Z4fUUCfnuDPCya7ysJ8Dr6ozwcp8Ar/dngJf5hHh9OCO8/q98jPLlkmYxZOrdf8sS2W/sX6LUlDcxoERu/xqaVdUMUK2t1tFBX9TaGnhpF//6mww9fuDwY/ib/x39LoZ2jeHAbnW1D44Kn8GLjAmhXkpV/f5RlQ88jlnWvqPZ35meIvQjgC+LlEe8atFKJZ3XWYVPAqbuxN2b/oKxQr6xPmdfSpoJ+QWuljl4QfSi7PIxysJ+lIUnQlmzrZoNZd7ZUVZn2UWHsqgfZdGJUDbocHZ+aXahObvscBb34yw+Ec46OyOxzpWz9x3OWD/O2Ilw1vmOYeCeHWfvNWdXHc5m/TibnQhn3Tw7P86uNGfvOpwl/ThLToSzznE2PjvKLh9Ls3k/yuYnQll3azy/4+ztY2nG+3HGT5UzcnaU1Tf9Dx3K7vpRdneqlP1omhH31yHtw2N5tuhH2uJESOtcQX7wRf0Lcta96qf9OEtPhLPOk9r8tTgbHf5lWP3zRf1/hK/+AVBLBwiCwErplwYAAOQoAABQSwECFAAUAAgICABweYxC1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAgIAHB5jEKCwErplwYAAOQoAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAALgcAAAAA" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />
+
<br/><br/><br/>
−
Schrägbild eines Würfels
+
'''
−
 
+
<span style="color: red">'''Vorgehensweise zum Zeichnen eines Schrägbildes'''</span>
−
 
+
: 1. Zeichne die Vorderfläche in wahrer Größe<br/>
−
 
+
: 2. Zeichne nach hinten verlaufende Kanten (Tiefenkanten) um 45° geneigt, um einen dreidimensionalen Effekt zu erreichen. Konstruiere die Kanten zudem nur halb so lang wie das vorgegebene Maß. <br/>
 +
: 3. Zeichne nicht sichtbare Kanten gestrichelt um den räumlichen Eindruck zu verstärken.
 +
 +
'''
 +
<br/><br/>
 
</div>
 
</div>
  
Zeile 27: Zeile 205:
 
|<div style="font: 10pt Verdana; font-weight:bold; padding:5px; border-bottom:1px solid #AAAAAA;">&nbsp;<big> <colorize> Aufgaben </colorize> </big>
 
|<div style="font: 10pt Verdana; font-weight:bold; padding:5px; border-bottom:1px solid #AAAAAA;">&nbsp;<big> <colorize> Aufgaben </colorize> </big>
 
</div>
 
</div>
−
<div class="multiplechoice-quiz">
 
  
−
Frage 1
+
<quiz display="simple">
−
(! A)
+
{ '''Aufgabe'''
−
( B)
+
| type="{}"}
−
(! C)
+
  
−
Frage 2
+
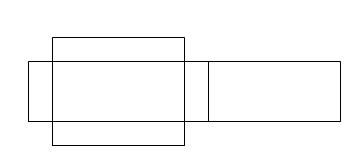
[[Datei:Aufgabe 1 Netz.jpg]] <br /> <br />
−
(! 1)
+
a) Aus welchen Formen setzt sich dieses Netz zusammen? { Rechteck | Dreieck | Quadrat } { Dreieck | Rechteck | Quadrat }
−
(! 2)
+
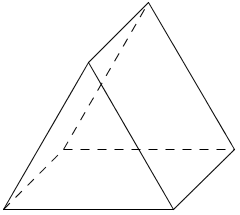
b) Wie heißt der Körper, der sich damit bauen lässt? { Prisma }
−
( 3)
+
c) Wie viele Kanten besitzt dieser Körper? { 9 }
 +
d) Wie viele Ecken besitzt dieser Körper?  { 6 }
 +
e) Zeichne ein Schrägbild des zum Netzt gehörigen Körpers.<br />
 +
</quiz>
  
−
</div>
+
<popup name="Lösung des Schrägbildes">
 +
[[Datei:Lösung Prisma Schrägbild.jpg]]<br />
 +
</popup>
  
  
 +
'''2.Zeichne drei Schrägbilder des Körpers, dessen Netz hier abgebildet ist, bei denen jedes Mal eine andere Quaderfläche vorne ist.''' <br /> <br />
 +
[[Datei:Netz1234.jpg]]
 +
 +
<br />
 +
<popup name="Lösung">
 +
 +
Drei mögliche Lösungen.<br />
 +
[[Datei:Lösung Schrägbild 1.jpg]] <br />
 +
[[Datei:Lösung Schrägbild 2.jpg]]<br />
 +
[[Datei:Lösung Schrägbild 3.jpg]]<br />
 +
</popup>
 +
 +
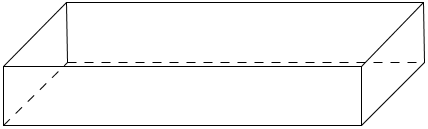
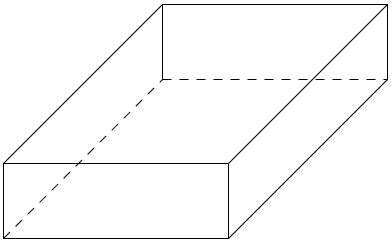
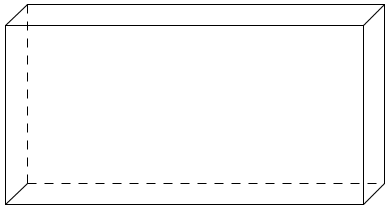
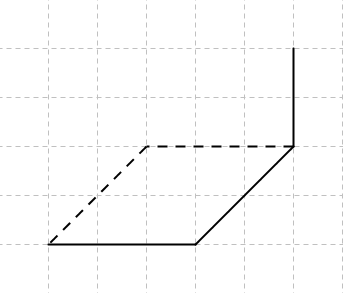
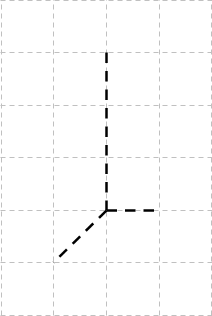
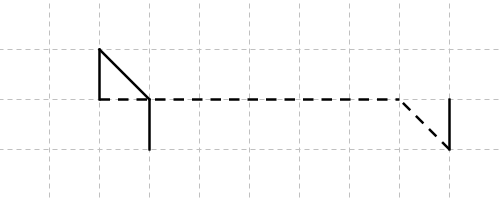
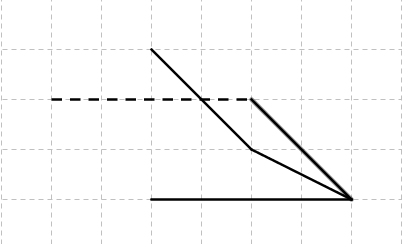
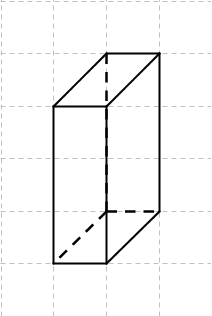
'''3.Zeichne folgende Schrägbilder fertig.'''<br />
 +
[[Datei:Schrägbild vervollständigen 1.jpg]]
 +
[[Datei:Schrägbild vervollständigen 2.jpg]]
 +
[[Datei:Schrägbild vervollständigen 3.jpg]]
 +
[[Datei:Schrägbild vervollständigen 4.jpg]]
 
&nbsp;
 
&nbsp;
−
<div class="lueckentext-quiz">
+
 
−
Texttexttext <strong>einfügen 1</strong> texttexttexttexttext <strong>einfügen 2</strong> text.</div>
+
 
 +
<popup name="Lösung">
 +
<br />
 +
[[Datei:Schrägbild vervollständigen 1 Lösung.jpg]]
 +
[[Datei:Schrägbild vervollständigen 2 Lösung.jpg]]
 +
[[Datei:Schrägbild vervollständigen 3 Lösung.jpg]]
 +
[[Datei:Schrägbild vervollständigen 4 Lösung.jpg]]
 +
 
 +
</popup>
 +
 
 +
 
  
  

Aktuelle Version vom 2. Dezember 2013, 15:17 Uhr

Erklärbär.PNGP-Seminar/Mathematik 2010-12
Hauptmenü
-----------------------------------------------------------------------------------
















 

IV. Geometrische Grundbegriffe:  

1. Geometrische Körper - 2. Geraden - 3. Abstände - 4. Parallelogramm - Umfang - 5. Kreise - 6. Winkel - 7. Achsensymmetrie - 8. Netze geometrischer Körper - 9. Schrägbilder


Erklärung

Als Schrägbild bezeichnet man einen Körper, der auf einer ebenen Fläche (z.B.einem Blatt Papier) aus schräger Perspektive 3-dimensional dargestellt wird.

Schrägbild Würfel.jpg

Schrägbild eines Würfels




Vorgehensweise zum Zeichnen eines Schrägbildes

1. Zeichne die Vorderfläche in wahrer Größe
2. Zeichne nach hinten verlaufende Kanten (Tiefenkanten) um 45° geneigt, um einen dreidimensionalen Effekt zu erreichen. Konstruiere die Kanten zudem nur halb so lang wie das vorgegebene Maß.
3. Zeichne nicht sichtbare Kanten gestrichelt um den räumlichen Eindruck zu verstärken.




  Aufgaben

1. Aufgabe

Aufgabe 1 Netz.jpg

a) Aus welchen Formen setzt sich dieses Netz zusammen?
b) Wie heißt der Körper, der sich damit bauen lässt?
c) Wie viele Kanten besitzt dieser Körper?
d) Wie viele Ecken besitzt dieser Körper?
e) Zeichne ein Schrägbild des zum Netzt gehörigen Körpers.

Punkte: 0 / 0



2.Zeichne drei Schrägbilder des Körpers, dessen Netz hier abgebildet ist, bei denen jedes Mal eine andere Quaderfläche vorne ist.

Netz1234.jpg


3.Zeichne folgende Schrägbilder fertig.
Schrägbild vervollständigen 1.jpg Schrägbild vervollständigen 2.jpg Schrägbild vervollständigen 3.jpg Schrägbild vervollständigen 4.jpg  






IV. Geometrische Grundbegriffe:  

1. Geometrische Körper - 2. Geraden - 3. Abstände - 4. Parallelogramm - Umfang - 5. Kreise - 6. Winkel - 7. Achsensymmetrie - 8. Netze geometrischer Körper - 9. Schrägbilder
\Rightarrow Weiter zum nächsten Themengebiet
Von „http://rmg.zum.de/index.php?title=P-Seminar/Mathematik_2010-12/IV.9._Schrägbilder&oldid=55276“