V.9. Abzählen am Baumdiagramm: Unterschied zwischen den Versionen
Aus RMG-Wiki
K (Umformulierung) |
|||
| (4 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
<imagemap> | <imagemap> | ||
Bild:Erklärbär.PNG|30px|left| | Bild:Erklärbär.PNG|30px|left| | ||
| − | rect 0 0 0 0 [[P-Seminar/Mathematik_2010-12 | + | rect 0 0 0 0 [[P-Seminar/Mathematik_2010-12]] |
| − | default [[P-Seminar/Mathematik_2010-12 | + | default [[P-Seminar/Mathematik_2010-12]] |
desc none | desc none | ||
</imagemap> | </imagemap> | ||
| Zeile 112: | Zeile 112: | ||
<div class="aussen"><div class="menutag">'''VI. Multiplikation und Division ganzer Zahlen'''</div> | <div class="aussen"><div class="menutag">'''VI. Multiplikation und Division ganzer Zahlen'''</div> | ||
| − | *[[P-Seminar/ | + | *[[P-Seminar/Mathematik 2010-12/VI.1. Multiplikation | 1. Multiplikation]] |
| − | *[[P-Seminar/ | + | *[[P-Seminar/Mathematik 2010-12/VI.2 Division | 2. Division]] |
| − | + | ||
</div> | </div> | ||
</div> | </div> | ||
| Zeile 161: | Zeile 161: | ||
<br><br><br><br> | <br><br><br><br> | ||
| + | |||
</div> | </div> | ||
| − | |||
| + | </div> | ||
</div> | </div> | ||
| Zeile 182: | Zeile 183: | ||
<br /> | <br /> | ||
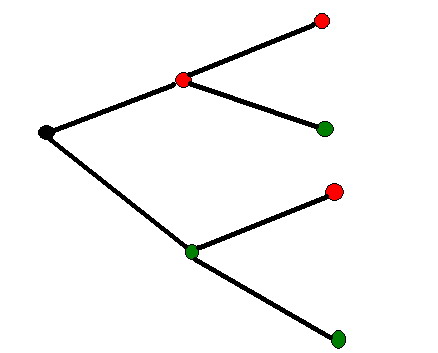
'''Baumdiagramm''' | '''Baumdiagramm''' | ||
| − | : Ein Baumdiagramm ist eine Grafik zum herausfinden aller Möglichkeiten | + | :Ein Baumdiagramm ist eine Grafik zum herausfinden aller Möglichkeiten. |
| − | + | :Das nachfolgende Baumdiagramm zeigt die Möglichkeiten, die es gibt um 3 Schülern auf einem Foto anzuordnen. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | [[Datei:baumdiagramm.jpg]] | |
Aktuelle Version vom 16. Dezember 2013, 15:27 Uhr
V. Multiplikation und Division natürlicher Zahlen:
Erklärung
Baumdiagramm
- Ein Baumdiagramm ist eine Grafik zum herausfinden aller Möglichkeiten.
- Das nachfolgende Baumdiagramm zeigt die Möglichkeiten, die es gibt um 3 Schülern auf einem Foto anzuordnen.
Merke:
Die letzte Reihe/Spalte ist die maximale Anzahl.
Aufgaben
Man will auf einem Foto 4 Personen unterschiedlich ordnen. Wie viele Möglichkeiten gibt es? (!48 ) ( 24) (! 12) Herbert hat eine rote, eine blaue und zwei gelbe Ostereier in seinem Nest gefunden. Wie viele Möglichkeiten gibt es, drei von ihnen anzuordnen? (! 10) (! 8) ( 12)
Die Anzahl der verschiedenen Möglichkeiten 3 Schüler auf einem Bild anzuordnen ist 6 .
|
V. Multiplikation und Division natürlicher Zahlen: