IV.7. Achsensymmetrie: Unterschied zwischen den Versionen
Aus RMG-Wiki
K |
|||
| Zeile 186: | Zeile 186: | ||
Die Faltkante nennt man <span style="color: red">Symmetrieachse a</span>.<br /> | Die Faltkante nennt man <span style="color: red">Symmetrieachse a</span>.<br /> | ||
<br /><br /> | <br /><br /> | ||
| − | Diese Figuren sind | + | Diese Figuren sind achsensymmetrisch:<br /> |
[[Datei:AchsensymetrieStern.png]]<br /><br /> | [[Datei:AchsensymetrieStern.png]]<br /><br /> | ||
[[Datei:AchsensymetriePfeil.png]]<br /> | [[Datei:AchsensymetriePfeil.png]]<br /> | ||
<br /> | <br /> | ||
| − | Es gibt auch Figuren mit mehreren | + | Es gibt auch Figuren mit mehreren Symmetrieachsen:<br /> |
[[Datei:AchsensymetrieRechteck.png]]<br /> | [[Datei:AchsensymetrieRechteck.png]]<br /> | ||
<br /> | <br /> | ||
| − | Ein Kreis hat unendlich viele | + | Ein Kreis hat unendlich viele Symmetrieachsen:<br /> |
[[Datei:AchsensymetrieKreis.png]]<br /> | [[Datei:AchsensymetrieKreis.png]]<br /> | ||
Version vom 2. Dezember 2013, 15:00 Uhr
IV. Geometrische Grundbegriffe:
Erklärung
Eine Figur ist achsensymmetrisch, wenn man sie so falten kann,
dass ihre beiden Teile genau aufeinander passen.
Die Faltkante nennt man Symmetrieachse a.
Diese Figuren sind achsensymmetrisch:

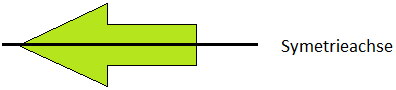
Es gibt auch Figuren mit mehreren Symmetrieachsen:
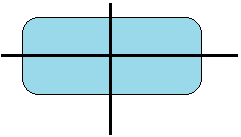
Ein Kreis hat unendlich viele Symmetrieachsen:
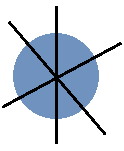
Aufgaben
|

