IV.5. Kreise: Unterschied zwischen den Versionen
| (19 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
<imagemap> | <imagemap> | ||
Bild:Erklärbär.PNG|30px|left| | Bild:Erklärbär.PNG|30px|left| | ||
| − | rect 0 0 0 0 [[P-Seminar/Mathematik_2010-12 | + | rect 0 0 0 0 [[P-Seminar/Mathematik_2010-12]] |
| − | default [[P-Seminar/Mathematik_2010-12 | + | default [[P-Seminar/Mathematik_2010-12]] |
desc none | desc none | ||
</imagemap> | </imagemap> | ||
| Zeile 112: | Zeile 112: | ||
<div class="aussen"><div class="menutag">'''VI. Multiplikation und Division ganzer Zahlen'''</div> | <div class="aussen"><div class="menutag">'''VI. Multiplikation und Division ganzer Zahlen'''</div> | ||
| − | *[[P-Seminar/ | + | *[[P-Seminar/Mathematik 2010-12/VI.1. Multiplikation | 1. Multiplikation]] |
| − | *[[P-Seminar/ | + | *[[P-Seminar/Mathematik 2010-12/VI.2 Division | 2. Division]] |
| − | + | ||
</div> | </div> | ||
</div> | </div> | ||
| Zeile 184: | Zeile 184: | ||
Alle Punkte eines '''Kreises''' haben von seinem '''Mittelpunkt''' den gleichen Abstand.<br /> | Alle Punkte eines '''Kreises''' haben von seinem '''Mittelpunkt''' den gleichen Abstand.<br /> | ||
Dieser Abstand heißt '''Radius''' des Kreises.<br /> | Dieser Abstand heißt '''Radius''' des Kreises.<br /> | ||
| − | Gibt man Mittelpunkt und Radius eines Kreises an, so kann er gezeichnet werden.<br /> | + | Gibt man Mittelpunkt und Radius eines Kreises an, so kann er gezeichnet werden. <br /><br /> |
[[Datei:Mittelpunkt,Radius,Durchmesser.png]] | [[Datei:Mittelpunkt,Radius,Durchmesser.png]] | ||
''' | ''' | ||
| Zeile 196: | Zeile 196: | ||
<div class="multiplechoice-quiz"> | <div class="multiplechoice-quiz"> | ||
| − | + | '''1. Welche Oberflächenfigur erhält man, wenn man einen ebenen Schnitt durch eine Kugel macht?''' | |
| − | (! | + | (! Quadrat) |
| − | ( | + | ( Kreis) |
| − | (! | + | (! Achteck) |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
</div> | </div> | ||
| − | + | '''2. Konstruktionsaufgabe'''<br /> | |
| − | + | Zeichne in ein Koordinatensystem die Punkte A(3/1), B(2/6), C(2/1), M(2/4). Zeichne einen Kreis um M mit dem Radius 3cm.<br /> | |
| + | [[:Angabe Lösung]] <br /> | ||
| + | a) Welche der Punkte A, B und C liegen innerhalb, außerhalb oder auf dem Kreis? <br /> | ||
| + | [[:Teilaufgabe a Lösung]] | ||
| + | <br /> b) Welchen Radius müsste der Kreis haben, damit B auf dem Kreis liegt? <br /> | ||
| + | [[:Teilaufgabe b Lösung]] | ||
| + | <br /> c) Gib jeweils einen Punkt aus dem zweiten Quadranten an, der innerhalb, außerhalb beziehungsweise auf dem Kreis liegt. Benenne diesen Punkt. | ||
| + | <br /><br /> | ||
| + | '''3. Textaufgabe''' <br /> | ||
| + | Du hast einen Tisch von 3 Metern Länge. <br /> | ||
| + | Wie viele Torten kannst du auf diesem Tisch maximal nebeneinander legen, wenn eine Torte einen Radius von 15cm besitzt? <br /> | ||
| + | [[:Aufgabe 3 Lösung]] | ||
| | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|}<noinclude> | |}<noinclude> | ||
Aktuelle Version vom 2. Dezember 2013, 14:45 Uhr
IV. Geometrische Grundbegriffe:
Erklärung
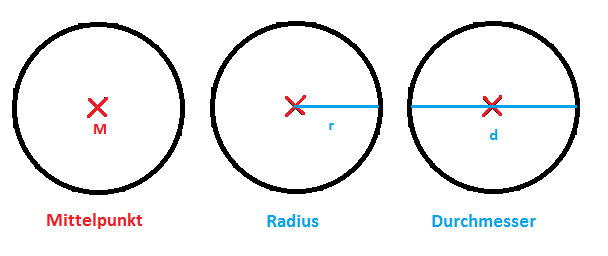
Alle Punkte eines Kreises haben von seinem Mittelpunkt den gleichen Abstand.
Dieser Abstand heißt Radius des Kreises.
Gibt man Mittelpunkt und Radius eines Kreises an, so kann er gezeichnet werden.
Aufgaben
1. Welche Oberflächenfigur erhält man, wenn man einen ebenen Schnitt durch eine Kugel macht? (! Quadrat) ( Kreis) (! Achteck) 2. Konstruktionsaufgabe |
IV. Geometrische Grundbegriffe:

