IV.6. Winkel: Unterschied zwischen den Versionen
Aus RMG-Wiki
| Zeile 225: | Zeile 225: | ||
</div> | </div> | ||
| − | '''Konstruktionsaufgabe''' <br /> | + | '''2. Konstruktionsaufgabe''' <br /> |
| − | Zeichne die Punkte A(6/4), B(0/1) und C(7/1) in ein Koordinatensystem. Verbinde die drei Punkte zum Dreieck ABC. Bezeichne die Winkel des Dreiecks mit griechischen Buchstaben und gib jeweils ihre Größe an. <br />[[:Konstruktionsaufgabe Lösung]] | + | a) Zeichne die Punkte A(6/4), B(0/1) und C(7/1) in ein Koordinatensystem. Verbinde die drei Punkte zum Dreieck ABC. <br /> |
| + | Bezeichne die Winkel des Dreiecks mit griechischen Buchstaben und gib jeweils ihre Größe an. <br /> | ||
| + | [[:Konstruktionsaufgabe Lösung]] | ||
| + | <div class="multiplechoice-quiz"> | ||
| + | Addiere die Innenwinkel des Dreiecks. | ||
| + | (! 90°) | ||
| + | ( 180°) | ||
| + | (! 240°) | ||
| + | </div> | ||
| | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
Version vom 10. September 2013, 16:03 Uhr
IV. Geometrische Grundbegriffe:
Erklärung
Winkel
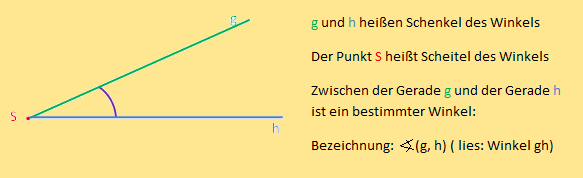
Winkel werden mit griechischen Buchstaben bezeichnet:
α: alpha.........β: beta.........γ:gamma.........δ: delta.........ε: epsilon.........φ: phi
Bestimmte Winkel:

Vergleich: Ein viertel Kreis
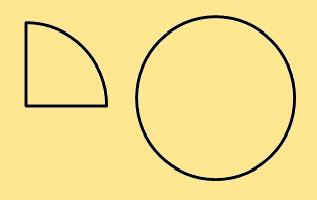
Aufgaben
Frage 1 (! A) ( B) (! C) Frage 2 (! 1) (! 2) ( 3) 2. Konstruktionsaufgabe Addiere die Innenwinkel des Dreiecks. (! 90°) ( 180°) (! 240°)
Texttexttext einfügen 1 texttexttexttexttext einfügen 2 text.
|
IV. Geometrische Grundbegriffe:

