IV.2. Geraden: Unterschied zwischen den Versionen
| Zeile 244: | Zeile 244: | ||
'''2. Konstruktionsaufgabe'''<br /><br /> | '''2. Konstruktionsaufgabe'''<br /><br /> | ||
| − | Gegeben sind die Punkte A(3/3), B(7/-1), C(4/0), D(-2/-3) [[:Datei:Lösung Angabe]]<br /> | + | Gegeben sind die Punkte A(3/3), B(7/-1), C(4/0), D(-2/-3) [[:Datei:Lösung Angabe]] <br /> |
| − | a) Zeichne eine Gerade g durch die Punkte A und B.<br /> | + | a) Zeichne eine Gerade g durch die Punkte A und B. [[:Lösung Teilaufgabe a]] <br /> |
| − | b) Zeichne die Strecke s, die durch die Punkte C und D festgelegt wird.<br /> | + | b) Zeichne die Strecke s, die durch die Punkte C und D festgelegt wird. [[:Lösung Teilaufgabe b]] <br /> |
| − | c) Zeichne eine Senkrechte e auf die Gerade g durch den Punkt D.<br /> | + | c) Zeichne eine Senkrechte e auf die Gerade g durch den Punkt D. [[:Lösung Teilaufgabe c]] <br /> |
| − | d) Bestimme die Koordinaten des | + | d) Bestimme die Koordinaten des Schnittpunktes E der Geraden g und e. [[:Lösung Teilaufgabe d]] <br /> |
| − | e) Zeichne die parallele Gerade zur Strecke s durch den Punkt E<br /> | + | e) Zeichne die parallele Gerade zur Strecke s durch den Punkt E [[:Lösung Teilaufgabe e]] <br /> |
<br /> | <br /> | ||
Version vom 26. Mai 2013, 14:06 Uhr
IV. Geometrische Grundbegriffe:
Erklärung
- Eine Gerade hat keinen Anfangspunkt und keinen Endpunkt.
- Eine Halbgerade (Strahl) hat einen Anfangspunkt, aber keinen Endpunkt.
- Eine Strecke ist von zwei Punkten begrenzt.
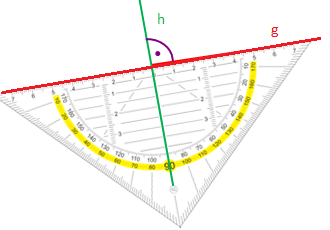
- Liegen zwei Geraden g und h wie im BildaksjjjdfhakdjsfSind zwei Geraden g und h senkrecht zu
- zueinander, so sagt man:aksdfhajjjhhhhhhhhhhhijijikdjsfeiner dritten Gerade k, so sagt man:
- g ist senkrecht zu hakshhhgdfhihihtdfhjijijijijihiakdjsfg und h sind zueinander parallel.
- oder: g ist orthogonal zu h.aksdfhfdvikakhdkjhgfedhijjsfMan schreibt dafür : g||h
- Man schreibt dafür: g
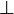 h
h
Aufgaben
1. Richtig oder Falsch? B A
E [AD] 2. Konstruktionsaufgabe 3. Zuordnung
|
IV. Geometrische Grundbegriffe:



 [AD]
( Richtig)
(!Falsch)
[AD]
( Richtig)
(!Falsch)
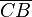 >
> 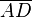 (!Richtig)
(Falsch)
(!Richtig)
(Falsch)
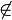 [AD]
(Richtig)
(!Falsch)
[AD]
(Richtig)
(!Falsch)
 [CB
(!Richtig)
(Falsch)
[CB
(!Richtig)
(Falsch)

