Die Aufgabe: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
K
Zeile 6: Zeile 6:
  
 
:a) aa) Untersuchen sie das Verhalten der Funktionen f<sub>a</sub> für t -> <math>\pm  \infty
 
:a) aa) Untersuchen sie das Verhalten der Funktionen f<sub>a</sub> für t -> <math>\pm  \infty
−
         </math> und geben sie für  
+
         </math> und geben sie für die Asymptoten Gleichungen an.
−
        die Asymptoten Gleichungen an.
+
  
 
[[Facharbeit Mathematik Straßheimer/Die Aufgabe/Lösung a) aa)|Hier gehts zur Lösung]]
 
[[Facharbeit Mathematik Straßheimer/Die Aufgabe/Lösung a) aa)|Hier gehts zur Lösung]]
  
−
::::ab) Zeigen sie, dass alle Funktionen f<sub>a</sub> monoton steigend sind.
+
:ab) Zeigen sie, dass alle Funktionen f<sub>a</sub> monoton steigend sind.
  
 
[[Facharbeit Mathematik Straßheimer/Die Aufgabe/Lösung a) ab)|Hier gehts zur Lösung]]
 
[[Facharbeit Mathematik Straßheimer/Die Aufgabe/Lösung a) ab)|Hier gehts zur Lösung]]
Zeile 19: Zeile 18:
 
[[Facharbeit Mathematik Straßheimer/Die Aufgabe/Lösung b) ba)|Hier gehts zur Lösung]]
 
[[Facharbeit Mathematik Straßheimer/Die Aufgabe/Lösung b) ba)|Hier gehts zur Lösung]]
  
−
::::bb) Jeder Graph G<sub>a</sub> bestitzt genau einen Wendepunkt W<sub>a</sub>
+
:bb) Jeder Graph G<sub>a</sub> bestitzt genau einen Wendepunkt W<sub>a</sub>
−
        Zeigen sie, dass die Wendepunkte W<sub>a</sub> auf einer parallelen zur t-Achse liegen.
+
::Zeigen sie, dass die Wendepunkte W<sub>a</sub> auf einer parallelen zur t-Achse liegen.
  
 
[[Facharbeit Mathematik Straßheimer/Die Aufgabe/Lösung b) bb)|Hier gehts zur Lösung]]
 
[[Facharbeit Mathematik Straßheimer/Die Aufgabe/Lösung b) bb)|Hier gehts zur Lösung]]
  
−
::::bc) Zeichnen sie die Graphen G<sub>0,75</sub> und G<sub>1</sub> in ein und dasselbe Koordinatensystem und  
+
:bc) Zeichnen sie die Graphen G<sub>0,75</sub> und G<sub>1</sub> in ein und dasselbe Koordinatensystem und schlussfolgern Sie, welchen Einfluss der Parameter a auf den Verlauf der Graphen G<sub>a</sub> hat.
−
        schlussfolgern Sie, welchen Einfluss der Parameter a auf den Verlauf der Graphen G<sub>a</sub> hat.
+
  
 
[[Facharbeit Mathematik Straßheimer/Die Aufgabe/Lösung b) bc)|Hier gehts zur Lösung]]
 
[[Facharbeit Mathematik Straßheimer/Die Aufgabe/Lösung b) bc)|Hier gehts zur Lösung]]
  
 
:c)    Der Graph G<sub>1</sub>, die t-Achse und die Gerade mit der Gleichung t = ln(29) begrenzen eine Fläche.
 
:c)    Der Graph G<sub>1</sub>, die t-Achse und die Gerade mit der Gleichung t = ln(29) begrenzen eine Fläche.
−
        Berechnen Sie die Maßzahl des Inhalts dieser Fläche.
+
::Berechnen Sie die Maßzahl des Inhalts dieser Fläche.
  
 
[[Facharbeit Mathematik Straßheimer/Die Aufgabe/Lösung c)|Hier gehts zur Lösung]]
 
[[Facharbeit Mathematik Straßheimer/Die Aufgabe/Lösung c)|Hier gehts zur Lösung]]
Zeile 40: Zeile 38:
 
[[Facharbeit Mathematik Straßheimer/Die Aufgabe/Lösung d) da)|Hier gehts zur Lösung]]
 
[[Facharbeit Mathematik Straßheimer/Die Aufgabe/Lösung d) da)|Hier gehts zur Lösung]]
  
−
::::db) Berchnen Sie, wann die Wachstumsgeschwindigkeit einer Sonnenblumenpflanze am größten ist.
+
:db) Berchnen Sie, wann die Wachstumsgeschwindigkeit einer Sonnenblumenpflanze am größten  
  
 
[[Facharbeit Mathematik Straßheimer/Die Aufgabe/Lösung d) db)|Hier gehts zur Lösung]]
 
[[Facharbeit Mathematik Straßheimer/Die Aufgabe/Lösung d) db)|Hier gehts zur Lösung]]
  
−
::::dc) Erläutern Sie die Grenzen dieser mathematischen Modellbildung.
+
:dc) Erläutern Sie die Grenzen dieser mathematischen Modellbildung.
  
 
[[Facharbeit Mathematik Straßheimer/Die Aufgabe/Lösung d) dc)|Hier gehts zur Lösung]]
 
[[Facharbeit Mathematik Straßheimer/Die Aufgabe/Lösung d) dc)|Hier gehts zur Lösung]]

Version vom 6. Januar 2010, 13:20 Uhr

Gegeben sind die Funktionen fa durch 

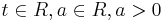
     y = f_{a}(t) = \frac{2\cdot e^{at}}{e^{at}+29}, t\in R, a\in R, a>0

Ihre Graphen werden mit Ga bezeichnet.

a) aa) Untersuchen sie das Verhalten der Funktionen fa für t -> 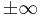\pm \infty und geben sie für die Asymptoten Gleichungen an.

Hier gehts zur Lösung

ab) Zeigen sie, dass alle Funktionen fa monoton steigend sind.

Hier gehts zur Lösung

b) ba) Untersuchen sie die Funktionen fa auf Nullstellen und lokale Extremstellen.

Hier gehts zur Lösung

bb) Jeder Graph Ga bestitzt genau einen Wendepunkt Wa
Zeigen sie, dass die Wendepunkte Wa auf einer parallelen zur t-Achse liegen.

Hier gehts zur Lösung

bc) Zeichnen sie die Graphen G0,75 und G1 in ein und dasselbe Koordinatensystem und schlussfolgern Sie, welchen Einfluss der Parameter a auf den Verlauf der Graphen Ga hat.

Hier gehts zur Lösung

c) Der Graph G1, die t-Achse und die Gerade mit der Gleichung t = ln(29) begrenzen eine Fläche.
Berechnen Sie die Maßzahl des Inhalts dieser Fläche.

Hier gehts zur Lösung

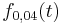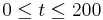Durch die Funktion f_{0,04}(t) für 0\leq t\leq 200 (t in Tagen) kann das Wachstum von Sonnenblumen beschrieben werden, wobei 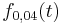f_{0,04}(t) die Höhe (in m) der Pflanzen zur Zeit t bedeutet.

d) da) Berechnen Sie die Höhe einer Sonnenblumenpflanze nach 10, 50 und 150 Tagen.

Hier gehts zur Lösung

db) Berchnen Sie, wann die Wachstumsgeschwindigkeit einer Sonnenblumenpflanze am größten

Hier gehts zur Lösung

dc) Erläutern Sie die Grenzen dieser mathematischen Modellbildung.

Hier gehts zur Lösung

Von „http://rmg.zum.de/index.php?title=Facharbeit_Mathematik_Straßheimer/Die_Aufgabe&oldid=25807“