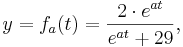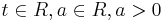Die Aufgabe: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
 
(15 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 1: Zeile 1:
 +
Die Folgende Aufgabe ist aus einer LK ABITURPRÜFUNG aus dem Jahre 2004 in Sachsen-Anhalt.
 +
 +
Sie sollte von euch in jedem Fall zuerst bearbeitet werden und anschließend erst mit Hilfe der Links zu den Lösungen seine eigenen Ergebnisse kontrolliert werden. Für diejenigen, die sich sehr sicher sind, stehen die Lösungen der Aufgaben zusammengefasst unter der jeweiligen Teilaufgabe. Diese sollten allerdings in jedem Fall erst nach Lösung der Aufgabe aufgedeckt werden.
 +
 +
<br />
 
Gegeben sind die Funktionen f<sub>a</sub> durch
 
Gegeben sind die Funktionen f<sub>a</sub> durch
  
−
      <math>y = f_{a}(t) = \frac{2\cdot e^{at}}{e^{at}+29}</math>, <math>t\in R, a\in R, a>0</math>
+
::<math>y = f_{a}(t) = \frac{2\cdot e^{at}}{e^{at}+29},\;\;\;\;\;</math> <math>t\in R, a\in R, a>0</math>
  
 
Ihre Graphen werden mit G<sub>a</sub> bezeichnet.
 
Ihre Graphen werden mit G<sub>a</sub> bezeichnet.
  
−
:a) aa) Untersuchen sie das Verhalten der Funktionen f<sub>a</sub> für t -> <math>\pm  \infty
+
a)  
−
        </math> und geben sie für die Asymptoten Gleichungen an.
+
:* Untersuchen sie das Verhalten der Funktionen f<sub>a</sub> für t gegen <math>\pm  \infty</math> und geben sie für die Asymptoten Gleichungen an.
−
 
+
−
[[Facharbeit Mathematik Straßheimer/Die Aufgabe/Lösung a) aa)|Hier gehts zur Lösung]]
+
  
−
:ab) Zeigen sie, dass alle Funktionen f<sub>a</sub> monoton steigend sind.
+
:* Zeigen sie, dass alle Funktionen f<sub>a</sub> monoton steigend sind.
 +
 +
::{{Lösung versteckt|
 +
- Für <math>- \infty</math> geht der Grenzwert gegen 0 und für <math>+ \infty</math> geht er gegen 2<br />
 +
- Es gibt 2 waagrechte Asymptoten mit den Gleichungen <math>a(x) = 0\;</math> und <math>b(x) = 2\;</math><br />
 +
- Der Graph der Funktion ist streng monoton steigend
 +
}}
  
−
[[Facharbeit Mathematik Straßheimer/Die Aufgabe/Lösung a) ab)|Hier gehts zur Lösung]]
+
[[Facharbeit Mathematik Straßheimer/Die Aufgabe/Lösung a)|Hier geht's zum Lösungsweg]]
  
−
:b) ba) Untersuchen sie die Funktionen f<sub>a</sub> auf Nullstellen und lokale Extremstellen.
+
b)
 +
:* Untersuchen sie die Funktionen f<sub>a</sub> auf Nullstellen und lokale Extremstellen.
  
−
[[Facharbeit Mathematik Straßheimer/Die Aufgabe/Lösung b) ba)|Hier gehts zur Lösung]]
+
:* Jeder Graph G<sub>a</sub> bestitzt genau einen Wendepunkt W<sub>a</sub>. Zeigen sie, dass die Wendepunkte W<sub>a</sub> auf einer parallelen zur t-Achse liegen.
  
−
:bb) Jeder Graph G<sub>a</sub> bestitzt genau einen Wendepunkt W<sub>a</sub>
+
:* Zeichnen sie die Graphen G<sub>0,75</sub> und G<sub>1</sub> in ein und dasselbe Koordinatensystem und schlussfolgern Sie, welchen Einfluss der Parameter a auf den Verlauf der Graphen G<sub>a</sub> hat.
−
::Zeigen sie, dass die Wendepunkte W<sub>a</sub> auf einer parallelen zur t-Achse liegen.
+
  
−
[[Facharbeit Mathematik Straßheimer/Die Aufgabe/Lösung b) bb)|Hier gehts zur Lösung]]
+
::{{Lösung versteckt|
 +
- Die Funktion bestitzt keine Nullstellen und Extrempunkte<br />
 +
- Der Wendepunkt liegt bei <math>(\frac {ln29}{a}|1)</math>; anhand des y-Wertes lässt sich die Unabhängigkeit von a erkennen, dass alle Wendepunkte W<sub>a</sub> auf einer Parallen zur t-Achse liegen
 +
}}
  
−
:bc) Zeichnen sie die Graphen G<sub>0,75</sub> und G<sub>1</sub> in ein und dasselbe Koordinatensystem und schlussfolgern Sie, welchen Einfluss der Parameter a auf den Verlauf der Graphen G<sub>a</sub> hat.
+
[[Facharbeit Mathematik Straßheimer/Die Aufgabe/Lösung b)|Hier geht's zum Lösungsweg]]
  
−
[[Facharbeit Mathematik Straßheimer/Die Aufgabe/Lösung b) bc)|Hier gehts zur Lösung]]
+
c)   
 +
:* Der Graph G<sub>1</sub>, die t-Achse und die Gerade mit der Gleichung <math>t = ln(29)\;</math> begrenzen eine Fläche. Berechnen Sie die Maßzahl des Inhalts dieser Fläche.
  
−
:c)    Der Graph G<sub>1</sub>, die t-Achse und die Gerade mit der Gleichung t = ln(29) begrenzen eine Fläche.
+
::{{Lösung versteckt|
−
::Berechnen Sie die Maßzahl des Inhalts dieser Fläche.
+
- Der Flächeninhalt geht gegen den Wert <math>A = 2\cdot ln2</math>
 +
}}
  
−
[[Facharbeit Mathematik Straßheimer/Die Aufgabe/Lösung c)|Hier gehts zur Lösung]]
+
[[Facharbeit Mathematik Straßheimer/Die Aufgabe/Lösung c)|Hier geht's zum Lösungsweg]]
  
−
Durch die Funktion <math>f_{0,04}(t)</math> für <math>0\leq t\leq 200</math> (t in Tagen) kann das Wachstum von Sonnenblumen beschrieben werden, wobei <math>f_{0,04}(t)</math> die Höhe (in m) der Pflanzen zur Zeit t bedeutet.
 
  
−
:d) da) Berechnen Sie die Höhe einer Sonnenblumenpflanze nach 10, 50 und 150 Tagen.
+
Durch die Funktion <math>f_{0,04}(t)\;</math> für <math>0\leq t\leq 200</math> (t in Tagen) kann das Wachstum von Sonnenblumen beschrieben werden, wobei <math>f_{0,04}(t)\;</math> die Höhe (in m) der Pflanzen zur Zeit t bedeutet.
  
−
[[Facharbeit Mathematik Straßheimer/Die Aufgabe/Lösung d) da)|Hier gehts zur Lösung]]
+
d)  
 +
:* Berechnen Sie die Höhe einer Sonnenblumenpflanze nach 10, 50 und 150 Tagen.
  
−
:db) Berchnen Sie, wann die Wachstumsgeschwindigkeit einer Sonnenblumenpflanze am größten  
+
:* Berchnen Sie, wann die Wachstumsgeschwindigkeit einer Sonnenblumenpflanze am größten  
  
−
[[Facharbeit Mathematik Straßheimer/Die Aufgabe/Lösung d) db)|Hier gehts zur Lösung]]
+
:* Erläutern Sie die Grenzen dieser mathematischen Modellbildung.
  
−
:dc) Erläutern Sie die Grenzen dieser mathematischen Modellbildung.
+
::{{Lösung versteckt|
 +
- Nach 10 Tagen ist die Sonnenblume 9,8cm hoch, nach 50 Tagen ist sie 40,6cm hoch und nach 150 Tagen ist sie 186,6cm hoch<br />
 +
- Die Wachstumsgeschwindigkeit ist am Wendepunkt WP am größten; dieser ist nach ca. 84 Tagen erreicht
 +
}}
  
−
[[Facharbeit Mathematik Straßheimer/Die Aufgabe/Lösung d) dc)|Hier gehts zur Lösung]]
+
[[Facharbeit Mathematik Straßheimer/Die Aufgabe/Lösung d)|Hier geht's zum Lösungsweg]]

Aktuelle Version vom 28. Januar 2010, 22:19 Uhr

Die Folgende Aufgabe ist aus einer LK ABITURPRÜFUNG aus dem Jahre 2004 in Sachsen-Anhalt.

Sie sollte von euch in jedem Fall zuerst bearbeitet werden und anschließend erst mit Hilfe der Links zu den Lösungen seine eigenen Ergebnisse kontrolliert werden. Für diejenigen, die sich sehr sicher sind, stehen die Lösungen der Aufgaben zusammengefasst unter der jeweiligen Teilaufgabe. Diese sollten allerdings in jedem Fall erst nach Lösung der Aufgabe aufgedeckt werden.


Gegeben sind die Funktionen fa durch

y = f_{a}(t) = \frac{2\cdot e^{at}}{e^{at}+29},\;\;\;\;\; t\in R, a\in R, a>0

Ihre Graphen werden mit Ga bezeichnet.

a)

  • Untersuchen sie das Verhalten der Funktionen fa für t gegen 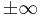\pm \infty und geben sie für die Asymptoten Gleichungen an.
  • Zeigen sie, dass alle Funktionen fa monoton steigend sind.

- Für 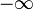- \infty geht der Grenzwert gegen 0 und für 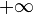+ \infty geht er gegen 2
- Es gibt 2 waagrechte Asymptoten mit den Gleichungen 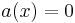a(x) = 0\; und b(x) = 2\;
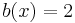
- Der Graph der Funktion ist streng monoton steigend

Hier geht's zum Lösungsweg

b)

  • Untersuchen sie die Funktionen fa auf Nullstellen und lokale Extremstellen.
  • Jeder Graph Ga bestitzt genau einen Wendepunkt Wa. Zeigen sie, dass die Wendepunkte Wa auf einer parallelen zur t-Achse liegen.
  • Zeichnen sie die Graphen G0,75 und G1 in ein und dasselbe Koordinatensystem und schlussfolgern Sie, welchen Einfluss der Parameter a auf den Verlauf der Graphen Ga hat.

- Die Funktion bestitzt keine Nullstellen und Extrempunkte
- Der Wendepunkt liegt bei 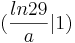(\frac {ln29}{a}|1); anhand des y-Wertes lässt sich die Unabhängigkeit von a erkennen, dass alle Wendepunkte Wa auf einer Parallen zur t-Achse liegen

Hier geht's zum Lösungsweg

c)

  • Der Graph G1, die t-Achse und die Gerade mit der Gleichung 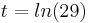t = ln(29)\; begrenzen eine Fläche. Berechnen Sie die Maßzahl des Inhalts dieser Fläche.

- Der Flächeninhalt geht gegen den Wert 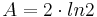A = 2\cdot ln2

Hier geht's zum Lösungsweg


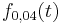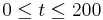Durch die Funktion f_{0,04}(t)\; für 0\leq t\leq 200 (t in Tagen) kann das Wachstum von Sonnenblumen beschrieben werden, wobei 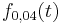f_{0,04}(t)\; die Höhe (in m) der Pflanzen zur Zeit t bedeutet.

d)

  • Berechnen Sie die Höhe einer Sonnenblumenpflanze nach 10, 50 und 150 Tagen.
  • Berchnen Sie, wann die Wachstumsgeschwindigkeit einer Sonnenblumenpflanze am größten
  • Erläutern Sie die Grenzen dieser mathematischen Modellbildung.

- Nach 10 Tagen ist die Sonnenblume 9,8cm hoch, nach 50 Tagen ist sie 40,6cm hoch und nach 150 Tagen ist sie 186,6cm hoch
- Die Wachstumsgeschwindigkeit ist am Wendepunkt WP am größten; dieser ist nach ca. 84 Tagen erreicht

Hier geht's zum Lösungsweg

Von „http://rmg.zum.de/index.php?title=Facharbeit_Mathematik_Straßheimer/Die_Aufgabe&oldid=28558“