Leonhard Euler/Wissenswertes
Aus RMG-Wiki
Die Euler'sche Zahl e als Basis der natürlichen Exponentialfunktion
Dieser Grenzwert ist vom Herleiten der Ableitung der Exponentialfunktion bekannt und wird deshalb als Euler'sche Zahl e bezeichnet. |
Merkmale der natürlichen Exponentialfunktion f(x)=ex
|
Die natürliche Exponentialfunktion und ihre Verschiebung
|
Wissenswertes |
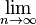 (1+
(1+ )n
)n  e hat der Funktionswert an der Stelle x=0 immer den Wert 1, denn a
e hat der Funktionswert an der Stelle x=0 immer den Wert 1, denn a R.
R. 
