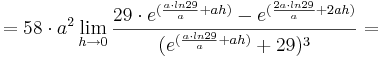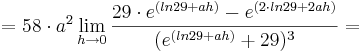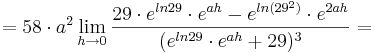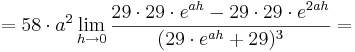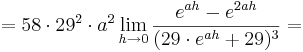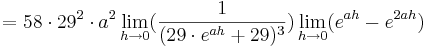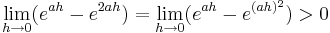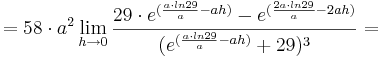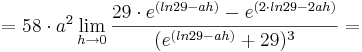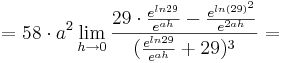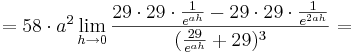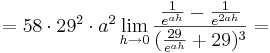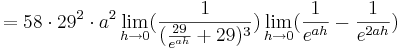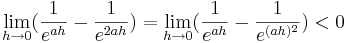H-Methode
2. Möglichkeit: Die h-Methode
Man nähert sich dem möglichen Wendepunkt mit Hilfe eines Grenzwertes an und versucht herauszufinden, ob ein Vorzeichenwechsel am Wendepunkt stattfindet. Dies kann man daran erkennen, ob das Vorzeichen, des Termes, den man gerade betrachtet, positiv oder negativ ist. Aufgrund dessen wird diese Variante in zwei verschiedene Teile aufgespalten. Man schaut sich zunächst im 1. Teil den Grenzwert von 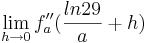 an und anschließend im 2. Teile den Grenzwert von
an und anschließend im 2. Teile den Grenzwert von 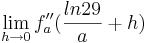 .
.
1. Teil: Betrachtung des Grenzwertes 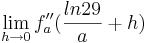
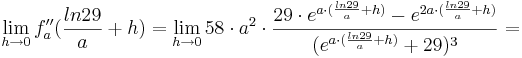
Da die Faktoren 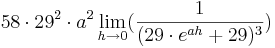 alle positiv sind, wird im folgenden nur noch das letzte Termglied betrachtet:
alle positiv sind, wird im folgenden nur noch das letzte Termglied betrachtet:
Das Termglied ist größer 0, da gilt: 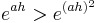 ; dies liegt daran, dass der Faktor
; dies liegt daran, dass der Faktor 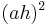 durch das Quadrat noch kleiner wird und somit der Term noch stärker gegen 0 strebt.
durch das Quadrat noch kleiner wird und somit der Term noch stärker gegen 0 strebt.
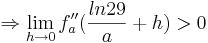
2. Teil: Betrachtung des Grenzwertes 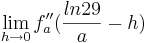
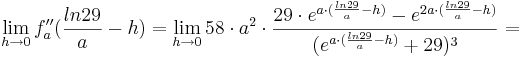
Da die Faktoren 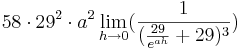 alle positiv sind, wird im folgenden wiederum nur der letzte verbliebene Teil des Terms betrachtet:
alle positiv sind, wird im folgenden wiederum nur der letzte verbliebene Teil des Terms betrachtet:
Der Term ist kleiner 0, da gilt: 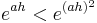 ; dies liegt daran, dass der Faktor
; dies liegt daran, dass der Faktor 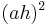 durch das Quadrat noch kleiner wird und somit der Term noch stärker gegen 0 strebt. Da jedoch nun die Kehrwerte gebildet werden, wird der Term
durch das Quadrat noch kleiner wird und somit der Term noch stärker gegen 0 strebt. Da jedoch nun die Kehrwerte gebildet werden, wird der Term 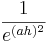 größer als der Term
größer als der Term 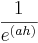 .
.
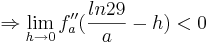
Zusammenführung der Teilergebnisse zum Endergebnis:
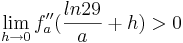
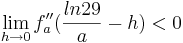
Man kann ganz leicht sehen, dass es einen Vorzweichenwechsel von Positiv zu Negativ an der möglichen Wendestelle gibt. Somit ist klar, dass es nicht nur eine mögliche Wendestelle ist, sondern auf jeden Fall an dieser t-Koordinate ein Wendepunkt sein muss.
Klicke hier um wieder zur Übersicht der beiden zusätzlichen Verfahren zu kommen, oder hier klicken um wieder zur Lösung der Teilaufgabe b) zu gelangen.