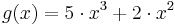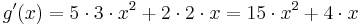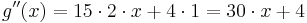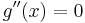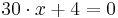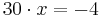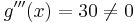Weitere Verfahren
Es gibt weiterhin zur Vorzeichentabelle noch 2 weitere Möglichkeiten der Überprüfung eines möglichen Wendepunktes. Diese sind hier im nachfolgenden aufgeführt:
2. Möglichkeit: Die h-Methode
Die h-Methode beweist im Grunde genommen den Vorzeichenwechsel an der möglichen Wendestelle, genau wie die Vorzeichentabelle. Allerdings wird bei der h-Methode nicht der Funktionsterm in seine Linearfaktoren aufgespalten und das Verhalten vor der möglichen Wendestelle überprüft, sondern mit Hilfe eines Grenzwertes sich der möglichen Wendestelle angenähert. Wenn man sich der Stelle nun von beiden Seiten nähert, kann man einen möglichen Vorzeichenwechsel sehr leicht feststellen.
Die h-Methode ist ebenfalls zum Nachweis für mögliche Extremstellen geeignet, allerdings ist hierbei darauf zu achten, dass das ganze mit der 1. Ableitung anstatt der 2. Ableitung durchzuführen ist. Weiterhin muss man aufpassen, da es ebenfalls einen Terrassenpunkt geben kann, an der sich die Monotonie nicht ändert. Dies muss bei der Überprüfung einer Extremstelle mit Hilfe der H-Methode berücksichtigt werden.
3. Möglichkeit: Die 3. Ableitung
Die Möglichkeit der Überprüfung eines Wendepunkts mit Hilfe der 3. Ableitung ist meistens etwas zeitsparender, als die Überprüfung durch die H-Methode. Man muss lediglich die 3. Ableitung der Funktion bilden und in diese dann die mögliche Wendestelle einsetzen. Wenn man hierbei ein Ergebnis bekommt, welches ungleich 0 ist, ist dies ebenfalls ein eindeutiger Beweis, dass an dieser Stelle ein Wendepunkt auftritt.
Bei dieser Möglichkeit ist zu beachten, dass man oftmals abwägen sollte, ob es Sinn macht diese Möglichkeit zum Nachweis in Betracht zu ziehen. Bei unserer Funktion, die wir besprechen, macht es wenig Sinn, da der Funktionsterm sehr komplex ist, was meistens bei gebrochen Rationalen Funktionen der Fall ist. Allerdings kann dieses Nachweisverfahren bei einfachen Gleichungen durchaus zeitsparend verwendet werden.
Ein Beispiel:
Mögliche Wendestelle:
Überprüfung der Wendestelle:
Daraus lässt sich erkennen, dass bei 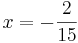 ein Wendepunkt zu finden ist.
ein Wendepunkt zu finden ist.
Bei solch einfachen Funktionen ist es deutlich von Vorteil diese Variante zu nehmen, da man die 2. Ableitung sehr schnell und leicht nochmals abgeleitet hat und man außerdem sofort erkennt, dass diese ungleich 0 ist.
Hier klicken um wieder zur Lösung der Aufgabe b) zu kommen