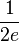Leonhard Euler/Abiturvorbereitung mit hilfreichen Links: Unterschied zwischen den Versionen
| Zeile 33: | Zeile 33: | ||
<br /> - Grenzwert x <math>\rightarrow</math> + <math>\infty</math>: '''lim g(x)= 0;''' | <br /> - Grenzwert x <math>\rightarrow</math> + <math>\infty</math>: '''lim g(x)= 0;''' | ||
</popup></div> | </popup></div> | ||
| − | <br /><br /><br /><br /><br /><br /><br /><br /> | + | <br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /> |
'''Abituraufgabe 2013 - Infinitesimalrechnung ''' | '''Abituraufgabe 2013 - Infinitesimalrechnung ''' | ||
<br /> | <br /> | ||
Aktuelle Version vom 4. November 2013, 18:58 Uhr
mit Lösungen
Veranschaulichung
Abituraufgabe 2012 - Infinitesimalrechnung
Gegeben ist die in R definierte Funktion g(x) = x e-2x.
e-2x.
Teilaufgabe Teil 1 2a (5 BE)
Bestimmen Sie die Koordinaten des Punkts, in dem der Graph von g eine waagrechte
Tangente hat.
Teilaufgabe Teil 1 2b (2 BE)
Geben Sie das Verhalten von g für x  -
-  und x
und x  +
+  an.
an.
Abituraufgabe 2013 - Infinitesimalrechnung
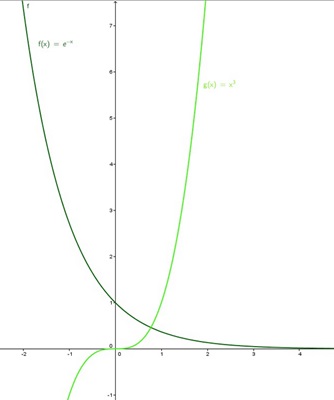
Gegeben sind die in R definierten Funktionen: g(x)=e-x und h(x)=x3;
Teilaufgabe Teil 1 3a (2 BE)
Veranschaulichen Sie durch eine Skizze, dass die Graphen g und h genau einen Schnittpunkt haben.
Teilaufgabe Teil 1 3b (4 BE)
Bestimmen Sie einen Nährungswert x1 für die x-Koordinate dieses Schnittpunkts, indem Sie für die in R
definierte Funktion d(x)=g(x)-h(x) den ersten Schritt des Newton-Verfahrens mit dem Startwert x0=1 durchführen.
Abiturvorbereitung mit hilfreichen Links