Lösung c): Unterschied zwischen den Versionen
Aus RMG-Wiki
(Die Seite wurde neu angelegt: Um den Flächeninhalt in dem Teilstück, welches der Graph G<sub>1</sub> mit der t-Achse und der Geraden mit der Gleichung <math>t = ln29 \;</math> einschließt, muss m...) |
K |
||
| Zeile 1: | Zeile 1: | ||
| + | <math>f_{1} (t) = \frac {2\cdot e^{t}} {e^{t} + 29}</math> | ||
| + | |||
Um den Flächeninhalt in dem Teilstück, welches der Graph G<sub>1</sub> mit der t-Achse und der Geraden mit der Gleichung <math>t = ln29 \;</math> einschließt, muss man das Integral mit der oberen Grenze <math>t = ln29 \;</math> und der unteren Grenze <math>- \infty </math> bilden. | Um den Flächeninhalt in dem Teilstück, welches der Graph G<sub>1</sub> mit der t-Achse und der Geraden mit der Gleichung <math>t = ln29 \;</math> einschließt, muss man das Integral mit der oberen Grenze <math>t = ln29 \;</math> und der unteren Grenze <math>- \infty </math> bilden. | ||
Zu beachten ist hierbei, dass ein Grenzwert benötigt wird, der gegen <math>- \infty</math> läuft, da man <math>- \infty </math> nicht für t einsetzen darf. | Zu beachten ist hierbei, dass ein Grenzwert benötigt wird, der gegen <math>- \infty</math> läuft, da man <math>- \infty </math> nicht für t einsetzen darf. | ||
| + | |||
| + | <math>A = \lim_{a \to -\infty } \int_a^{ln29} \! f_{1}(t) \, dt = </math> | ||
| + | :<math>= \lim_{a \to -\infty } \int_a^{ln29} \! \frac {2\cdot e^{t}} {e^{t} + 29} \, dt =</math> | ||
| + | :<math>= \lim_{a \to -\infty } \int_a^{ln29} \! 2\cdot \frac {e^{t}} {e^{t} + 29} \, dt =</math> | ||
| + | :<math>= \lim_{a \to -\infty } 2\cdot \int_a^{ln29} \! \frac {e^{t}} {e^{t} + 29} \, dt =</math> | ||
| + | :<math>= \lim_{a \to -\infty } 2\cdot \left[ln(e^{t} + 29)\right]_{a}^{ln29} =</math> | ||
| + | :<math>= 2\cdot [ln(29 + 29) - \lim_{a \to -\infty } ln(e^{a} + 29)] =</math> | ||
| + | :<math>= 2\cdot [ln58 - \lim_{a \to -\infty } ln(e^{a} + 29)] =</math> | ||
| + | :<math>= 2\cdot [ln58 - ln29] = 2\cdot ln(\frac {58} {29})= 2\cdot ln2</math> | ||
Version vom 25. Januar 2010, 18:56 Uhr
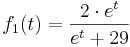
Um den Flächeninhalt in dem Teilstück, welches der Graph G1 mit der t-Achse und der Geraden mit der Gleichung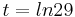 
einschließt, muss man das Integral mit der oberen Grenze 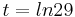und der unteren Grenze 
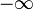bilden.
Zu beachten ist hierbei, dass ein Grenzwert benötigt wird, der gegen 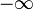läuft, da man 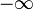nicht für t einsetzen darf.
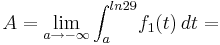
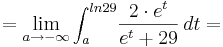
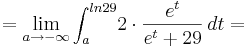
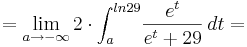
![= \lim_{a \to -\infty } 2\cdot \left[ln(e^{t} + 29)\right]_{a}^{ln29} =](/images/math/5/e/f/5ef69570e3c97ca6df07b2edee79eea9.png)
![= 2\cdot [ln(29 + 29) - \lim_{a \to -\infty } ln(e^{a} + 29)] =](/images/math/a/0/e/a0e5624221da6247f6d3e172d6c959cd.png)
![= 2\cdot [ln58 - \lim_{a \to -\infty } ln(e^{a} + 29)] =](/images/math/d/2/d/d2d45cfc74e48d48b7c7e0516e649e2e.png)
![= 2\cdot [ln58 - ln29] = 2\cdot ln(\frac {58} {29})= 2\cdot ln2](/images/math/c/c/d/ccda4d78945986989f6307e0c7884b4c.png)
