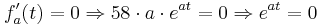Lösung a) ab): Unterschied zwischen den Versionen
Aus RMG-Wiki
(Die Seite wurde neu angelegt: <math>y = f_{a}(t) = \frac{2\cdot e^{at}}{e^{at}+29}</math>, <math>t\in R, a\in R, a>0</math> ==Zeigen Sie, dass alle Funktionen f<sub>a</sub> monoton steigend sind==...) |
|||
| Zeile 4: | Zeile 4: | ||
<math>f'_{a} (t) = \frac{2\cdot a\cdot e^{at}\cdot (e^{at} + 29) - 2\cdot e^{at}\cdot a\cdot e^{at} }{(e^{at}+29) ^{2} } = 2\cdot a\cdot \frac{(e^{at}) ^{2} + 29\cdot e^{at} - (e^{at}) ^{2} }{(e^{at}+29) ^{2}} = \frac{58\cdot a\cdot e^{at} }{(e^{at}+29) ^{2}} </math> | <math>f'_{a} (t) = \frac{2\cdot a\cdot e^{at}\cdot (e^{at} + 29) - 2\cdot e^{at}\cdot a\cdot e^{at} }{(e^{at}+29) ^{2} } = 2\cdot a\cdot \frac{(e^{at}) ^{2} + 29\cdot e^{at} - (e^{at}) ^{2} }{(e^{at}+29) ^{2}} = \frac{58\cdot a\cdot e^{at} }{(e^{at}+29) ^{2}} </math> | ||
| + | |||
| + | |||
| + | |||
| + | Suche nach möglichem Extrempunkt; falls kein Extrempunkt vorhanden ist, zeigt dies, dass die Funktion monoton steigend oder fallend sein muss. | ||
| + | |||
| + | <math>f'_{a}(t) = 0 \Rightarrow 58\cdot a\cdot e^{at} = 0 \Rightarrow e^{at} = 0</math> | ||
Version vom 3. Januar 2010, 17:33 Uhr
,
Zeigen Sie, dass alle Funktionen fa monoton steigend sind
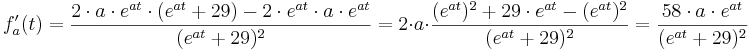
Suche nach möglichem Extrempunkt; falls kein Extrempunkt vorhanden ist, zeigt dies, dass die Funktion monoton steigend oder fallend sein muss.