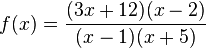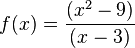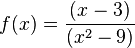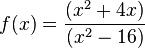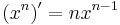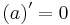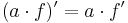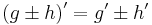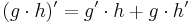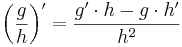Q11 Mathematik: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
Zeile 5: Zeile 5:
 
<center><table border="0" width="800px" cellpadding=5 cellspacing=15>
 
<center><table border="0" width="800px" cellpadding=5 cellspacing=15>
 
<tr><td  width="800px" valign="top">
 
<tr><td  width="800px" valign="top">
 +
===Hausaufgaben===
 +
[[Datei:Homework - vector maths.jpg|200px|right]]
 +
[[Q11 Mathematik/Hausaufgabenverbesserung|Was muss ich bei der HA-Verbesserung beachten?]]
  
−
==== Kurse 2015/2017 ====
+
===Kurse===
−
[[Q11 Mathematik/M5 2015_17|M5 SHE]]
+
2015/2017: [[Q11 Mathematik/M5 2015_17|M5 SHE]]
−
</td></tr></table></center>
+
  
−
</div>
+
2014/2016: [[Q11 Mathematik/M8 2014_16|M8 BEK]]
−
<div style="padding:1px;background: #EEEEE6;border:0px groove;">
+
  
−
 
+
2013/2015: [[Q11 Mathematik/M1 2013_15|M1 EIR]] -  [[Q11 Mathematik/M5 2013_15|M5 OBL]] - [[Q11 Mathematik/M6 2013_15|M6 SCU]]
−
<center><table border="0" width="800px" cellpadding=5 cellspacing=15>
+
−
<tr><td  width="800px" valign="top">
+
−
 
+
−
==== Kurse 2014/2016 ====
+
−
[[Q11 Mathematik/M8 2014_16|M8 BEK]]
+
−
</td></tr></table></center>
+
−
 
+
−
</div>
+
−
<div style="padding:1px;background: #EEEEE6;border:0px groove;">
+
−
 
+
−
 
+
−
<center><table border="0" width="800px" cellpadding=5 cellspacing=15>
+
−
<tr><td  width="800px" valign="top">
+
−
 
+
−
==== Kurse 2013/2015 ====
+
−
[[Q11 Mathematik/M1 2013_15|M1 EIR]] -  [[Q11 Mathematik/M5 2013_15|M5 OBL]] - [[Q11 Mathematik/M6 2013_15|M6 SCU]]
+
 
</td></tr></table></center>
 
</td></tr></table></center>
  

Version vom 15. September 2015, 23:28 Uhr


Hausaufgaben

Homework - vector maths.jpg

Was muss ich bei der HA-Verbesserung beachten?

Kurse

2015/2017: M5 SHE

2014/2016: M8 BEK

2013/2015: M1 EIR - M5 OBL - M6 SCU


1. Gebrochenrationale Funktionen

Gratfnk ok.png

Lösungen Buch:

12/10d - 12/10b - 13/12 - 13/15 - 16/2 - 17/9 - 21/3f - 21/4 - 26/3 - 26/4 - 24 - 25/10

Lösungen AH:

14/13 - 16/2b

Graphen einfacher gebrohenrationaler Funktionen

Arbeitsblatt

Videos: Kurvendiskussion zu den Funktionen (englisch)

f(x)=\frac{(3x+12)(x-2)}{(x-1)(x+5)} f(x)=\frac{(x^2-9)}{(x-3)} f(x)=\frac{(x-3)}{(x^2-9)} f(x)=\frac{(x^2+4x)}{(x^2-16)}


2. Differenzenquotient - mittlere Änderungsrate -Steigung Sekante

AccroissementMoyen.svg
  1. Film: Mittlere Änderungsrate
  2. Film: Durchschnittsgeschwindigkeit
  3. Film: Sekante
  4. Wiederholung: Lineare Funktionen
  5. Übung: Differenzenquotient
  6. Lösungen Buch: 30/7


3. Differentialquotient - lokale Änderungsrate - Steigung Tangente

Tangent.png
  1. Sekante --> Tangente
  2. Quiz zum Einstieg
  3. Film: Ableitung
  4. Film: Tangente
  5. Übung1
  6. Übung2
  7. Übung zur Ableitung
  8. Interaktiv: 34/5 - 39/10
  9. Lösungen Buch: 38/5c - 38/6 - 39/13 - 39/8c - 34/10a


4. Ableitungsfunktion

Derivative pic.svg
  1. Graph der Ableitungsfunktion LS Seite 41
  2. Der Graph der Ableitungsfunktion
  3. Übung zur Ableitungsfunktion
  4. Das Ableitungspuzzle
  5. Lösungen Buch: 42/2b - 42/2f - 42/5 - 43/10 - 42/3a - 43/9d


5. Ableitungsregeln

  1. Lösung Seite 51
  2. Lösung Seite 51/12 und 14
  3. Interaktiv: Seite 51/8
  4. Lösungen Buch: 48/2 und 51/4 - 48/2 und 3 - 48/6 und 62/1 - 52/10 - 52/15 - 61/6,7,9
\left(x^n\right)' = n x^{n-1}
\left(a\right)' = 0
(a\cdot f)' = a\cdot f'
\left(g \pm h\right)' = g' \pm h'
(g\cdot h)' = g' \cdot h + g \cdot h'
\left(\frac{g}{h}\right)' = \frac{g' \cdot h - g \cdot h'}{h^2}


6. Monotonie, Extrema, Funktionsuntersuchung

Extrema example.svg
  1. Musterbeispiele zur Monotonie
  2. Interaktiv: Extrema: Beispielaufgaben
  3. Funktionsuntersuchung: Musteraufgabe S74 Teil 1, Musteraufgabe S74 Teil 2
  4. Lösungen Buch: 66/5ceg - 66/5h - 67/8b -72/2 - 73/3 - 73/4 -73/6 - 77/3 - 79/17 -80/21


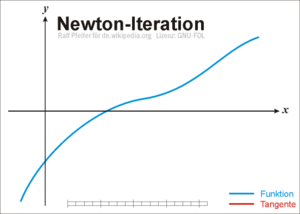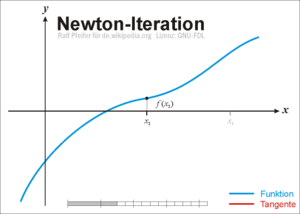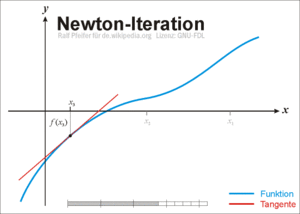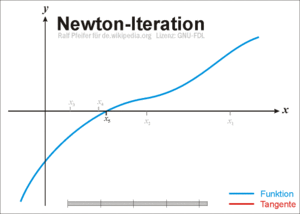
7. Newton-Verfahren

NewtonIteration Ani rmg.gif
  1. 88/5b
  2. Newton-Verfahren mit GeoGebra
  3. Animation
  4. Buch Seite 81
  5. Newton-Verfahren - Herleitung
  6. Newton-Algorithmus zur Approximation von Nullstellen
  7. Buch Seite 88/5c,d
  8. Lösungen Buch: 83/4a
Weiteres
  1. Visualisierung des Newton-Verfahrens mit Excel
  2. Das Newtonsche Näherungsverfahren ( Lindner)
  3. Applet von mathe-online


8. Analytische Geometrie

Arbeitsblätter
Programme zur Veranschaulichung
Vektoris3D Testversion
GeosekII, Vektor
Lösungen Buch: 124/1 - 124/4 - 105/11- 110/21- 116/5


9. Weitere Ableitungsregeln

Ableitung der Sinusfunktion
Applet mit Geogebra
Lösungen Buch: 127/3,4
Umkehrfunktion
Lösungen Buch: 129/15 b und c - 132/2, 3a,d 4a - 132/6a - 132/3 a)-d), 4 a)-c), 6 d)


10. Exponentialfunktion

Exp.png
  1. Arbeitsblatt Exponentialfunktion zur Basis a
  2. Interaktiv: Allgemeine Exponentialfunktion und ihre Ableitung
  3. Lernpfad zur Exponential- und Logarithmusfunktionen
  4. Die Eulersche Zahl
  5. Videos zur Kurvendiskussion


11. Wahrscheinlichkeitsbegriff und Unabhängigkeit

Venn-diagram-AB.png
  1. Verknüpfen von Ereignissen
  2. Unabhängigkeit
  3. Lösungen Buch: 185/4,8,15


  1. Extremwertaufgabe Schachtel
  2. Hühnerhof
  3. Wasserbehälter im Dach einer Mühle
  4. Maximales Dreieck
  5. Parallelogramm im Rechteck
  6. Rechteck mit größter Fläche aus Glasrest
  7. Lösung zu Hühnerhof_Mühle_Glasscheibe
  8. LS 221/7 weitere Lösung
  9. Lösungen Buch: Seite 202/5
Weiteres
  1. Extremwertaufgaben mit geogebra als Lernpfad
  2. Musterbeispiel: Einen Schrank um die Ecke bringen
  3. Lernpfad Extremwertaufgaben


13. Funktionen mit Parametern

  1. Saltoeinwurf
  2. Interaktiv: 222/2 - 222/4 - 214/8
  3. Ballwurf


14. Kurvendiskussion

Ableitungsss.svg
  1. Lernpfad zur Einführung in die Differentialrechnung 1
  2. Lernpfad zur Einführung in die Differentialrechnung 2
  3. Filmclip über die Grundidee des Differenzierens



ldv:Matemáticas 11

Von „http://rmg.zum.de/index.php?title=Q11_Mathematik&oldid=64626“