Leonhard Euler/Weiterführende Aufgaben: Unterschied zwischen den Versionen
| (12 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
1. Gebe den Funktionsterm der Funktion f(x) an, wenn... | 1. Gebe den Funktionsterm der Funktion f(x) an, wenn... | ||
<br /> | <br /> | ||
| − | * ... die e-Funktion um 5 Längeneinheiten nach oben verschoben wird und um 4 Längeneinheiten nach rechts. | + | * ... die e-Funktion um 5 Längeneinheiten nach oben verschoben wird und um 4 Längeneinheiten nach rechts. |
* ... die e-Funktion um 2 Längeneinheiten nach rechts verschoben wird und an der x-Achse gespiegelt wird. | * ... die e-Funktion um 2 Längeneinheiten nach rechts verschoben wird und an der x-Achse gespiegelt wird. | ||
* ... die e-Funktion um den Faktor 2 parallel zur x-Achse gestaucht wird. | * ... die e-Funktion um den Faktor 2 parallel zur x-Achse gestaucht wird. | ||
| Zeile 14: | Zeile 14: | ||
b) Wann hat sein Schwarm eine Größe von 5000 Fischen erreicht? | b) Wann hat sein Schwarm eine Größe von 5000 Fischen erreicht? | ||
<br /><br /><br /> | <br /><br /><br /> | ||
| − | 4. Die ideale Körpertemperatur vom Menschen liegt bei 36,5°C | + | 4. Die ideale Körpertemperatur vom Menschen liegt bei 36,5°C. <br /> |
Horst ist im Krankenhaus mit erhöhter Temperatur. Der Arzt beobachtet Horsts Temperatur 48 Stunden lang und hält diese in einem Diagramm fest. | Horst ist im Krankenhaus mit erhöhter Temperatur. Der Arzt beobachtet Horsts Temperatur 48 Stunden lang und hält diese in einem Diagramm fest. | ||
<br />Seine Erkenntnisse lassen sich mit folgendem Funktionsterm beschreiben: f(t)= 36,5+t<math>\cdot</math>e<sup>-0,3t</sup> | <br />Seine Erkenntnisse lassen sich mit folgendem Funktionsterm beschreiben: f(t)= 36,5+t<math>\cdot</math>e<sup>-0,3t</sup> | ||
| + | <br />t=Zeit in h; f(t)=Körpertemperatur in °C; <br /> | ||
| + | a) Skizziere den Graphen. <br /> | ||
| + | b) Berechne seine Höchsttemperatur innerhalb der ersten zwei Tage. <br /> | ||
| + | |||
| Zeile 38: | Zeile 42: | ||
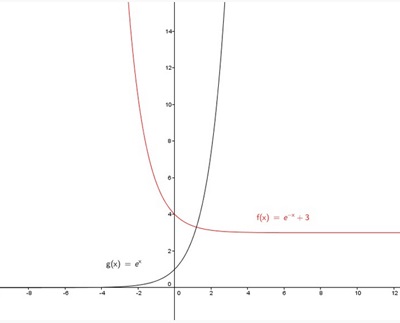
* Da x hier durch -x ersetzt wird, wird der Graph der e-Funktion an der y-Achse gespiegelt. Außerdem wird durch die Addition von 3 der Graph | * Da x hier durch -x ersetzt wird, wird der Graph der e-Funktion an der y-Achse gespiegelt. Außerdem wird durch die Addition von 3 der Graph | ||
parallel zur y-Achse um 3 Einheiten nach oben verschoben. <br /> | parallel zur y-Achse um 3 Einheiten nach oben verschoben. <br /> | ||
| − | [[ | + | [[Datei:Lösung_weiterfAufg_lisaRegr2.jpg]] |
</popup></div> | </popup></div> | ||
| Zeile 53: | Zeile 57: | ||
'''t = 21,4 Jahre''' | '''t = 21,4 Jahre''' | ||
</popup></div> | </popup></div> | ||
| + | <div style="float:left"><popup name="Lösung 4."> | ||
| + | a)[[Datei:Lösung_weiterfAufg_lisaRegr.jpg]] <br /> | ||
| + | b)Höchstemperatur: Hochpunkt; f(t)= 36,5+t<math>\cdot</math>e<sup>-0,3t</sup>; <br /> | ||
| + | Ableitung: f'(t)= -0,3t <math>\cdot</math>e<sup>-0,3t</sup>+e<sup>-0,3t</sup>= <br /> | ||
| + | =e<sup>-0,3t</sup><math>\cdot</math>(-0,3t+1); <br /> | ||
| + | ''Nullstellen der Ableitung bestimmen'': f'(t)=0; <br /> | ||
| + | e<sup>-0,3t</sup><math>\cdot</math>(-0,3t+1)=0; <br /> | ||
| + | e<sup>-0,3t</sup> wird nie Null. <br /> | ||
| + | -0,3t+1=0; <br /> 0,3t=1;<br /> | ||
| + | NS:'''t=3<math>\frac {1} {3}</math>''' | ||
| + | f(3<math>\frac {1} {3}</math>)='''37,73''';<br /> | ||
| + | |||
| + | </popup> </div> | ||
| + | |||
| + | |||
| + | |||
<br /><br /> | <br /><br /> | ||
<br /> | <br /> | ||
| − | <br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /> | + | <br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /> |
<div style="float:left"><div style="border: 1px solid #808000; background-color:#808000; font-size:1px; height:8px; border-bottom:1px solid #808000;"></div> | <div style="float:left"><div style="border: 1px solid #808000; background-color:#808000; font-size:1px; height:8px; border-bottom:1px solid #808000;"></div> | ||
<div style="border: 1px solid #808000; background-color:#F5F5DC; padding:30px;"> | <div style="border: 1px solid #808000; background-color:#F5F5DC; padding:30px;"> | ||
Aktuelle Version vom 7. November 2013, 21:30 Uhr
1. Gebe den Funktionsterm der Funktion f(x) an, wenn...
- ... die e-Funktion um 5 Längeneinheiten nach oben verschoben wird und um 4 Längeneinheiten nach rechts.
- ... die e-Funktion um 2 Längeneinheiten nach rechts verschoben wird und an der x-Achse gespiegelt wird.
- ... die e-Funktion um den Faktor 2 parallel zur x-Achse gestaucht wird.
2. Wie sieht der Graph der e-Funktion aus, wenn gilt: f(x)=-e-x + 3?
3.Fische vermehren sich in einem Biotop nach folgendem Funktionsterm:
f(x)= n0  e^
e^ 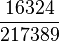
 t
t
n0= Anfangswert; t=Zeit in Jahren
Der Fischzüchter begann seine Zucht mit 1000 Fischen.
a) Wie groß ist der Schwarm nach 4,5 Jahren?
b) Wann hat sein Schwarm eine Größe von 5000 Fischen erreicht?
4. Die ideale Körpertemperatur vom Menschen liegt bei 36,5°C.
Horst ist im Krankenhaus mit erhöhter Temperatur. Der Arzt beobachtet Horsts Temperatur 48 Stunden lang und hält diese in einem Diagramm fest.
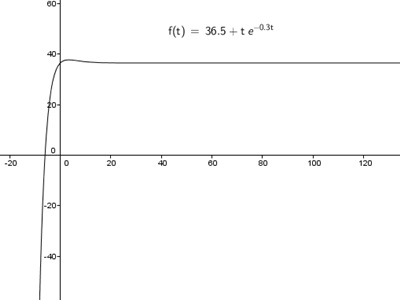
Seine Erkenntnisse lassen sich mit folgendem Funktionsterm beschreiben: f(t)= 36,5+t e-0,3t
e-0,3t
t=Zeit in h; f(t)=Körpertemperatur in °C;
a) Skizziere den Graphen.
b) Berechne seine Höchsttemperatur innerhalb der ersten zwei Tage.
Weiterführende Aufgaben
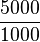 =
= 
 f(3
f(3
