Leonhard Euler/Einstiegsaufgaben: Unterschied zwischen den Versionen
Aus RMG-Wiki
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 8: | Zeile 8: | ||
<br>-''Steigung:'' f'(1)=5e+1; | <br>-''Steigung:'' f'(1)=5e+1; | ||
</popup> | </popup> | ||
| − | + | ||
| − | + | ||
{| border="0" cellpadding="5" cellspacing="2" style="border-left: 10px solid {{{RandLinks|#885}}}; margin-bottom: 0.4em; margin-left: auto; margin-right: auto; width: {{{Breite|100%}}}; background-color: {{{Hintergrund|#DEC}}}" | {| border="0" cellpadding="5" cellspacing="2" style="border-left: 10px solid {{{RandLinks|#885}}}; margin-bottom: 0.4em; margin-left: auto; margin-right: auto; width: {{{Breite|100%}}}; background-color: {{{Hintergrund|#DEC}}}" | ||
| Zeile 47: | Zeile 46: | ||
<br /> '''Finde die Stammfunktion zu den beiden gegebenen Funktionstermen!''' | <br /> '''Finde die Stammfunktion zu den beiden gegebenen Funktionstermen!''' | ||
<br /> 1. f<sub>1</sub>(x)= 5e<sup>2x</sup> | <br /> 1. f<sub>1</sub>(x)= 5e<sup>2x</sup> | ||
| − | <br /> 2. f<sub>2</sub>(x)= 3e<sup>2x+1</sup> | + | <br /> 2. f<sub>2</sub>(x)= 3e<sup>2x+1</sup><br /> |
| + | <popup name="Lösung"> | ||
| + | ''Zur Erinnerung:'' F'(x)=f(x); <br /> | ||
| + | 1. f<sub>1</sub>(x)= 5e<sup>2x</sup>; <br /> | ||
| + | '''F(x)=2,5e<sup>2x</sup>''' <br /><br /> | ||
| + | 2. f<sub>2</sub>(x)= 3e<sup>2x+1</sup>; <br /> | ||
| + | '''F(x)=1,5e<sup>2x+1</sup>''' | ||
| + | </popup> | ||
<div style="float:left"><div style="border: 1px solid #808000; background-color:#808000; font-size:1px; height:8px; border-bottom:1px solid #808000;"></div> | <div style="float:left"><div style="border: 1px solid #808000; background-color:#808000; font-size:1px; height:8px; border-bottom:1px solid #808000;"></div> | ||
Aktuelle Version vom 3. November 2013, 14:32 Uhr
Einstiegsaufgaben zur natürlichen Exponentialfunktion
Bestimmen Sie die Ableitungsfunktion der vorgegebenen Funktion f und berechnen Sie die Steigung des Graphen f an der Stelle x=1.
f(x)=5ex + x
|
Bei den Aufgaben zur Vereinfachung eines Termes sind oft die Potenzgesetze notwendig:
|
Differenziere folgende Funktionsterme!
1. f1(x)= e3x-8
2. f2(x)= ecosx  sinx
sinx
3. f3(x)= e-x
4. f4(x)= (x2- 4)ex
Finde die Stammfunktion zu den beiden gegebenen Funktionstermen!
1. f1(x)= 5e2x
2. f2(x)= 3e2x+1
Einstiegsaufgaben
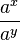 = ax-y
= ax-y
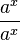 = (
= (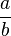 )x
)x

