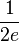Leonhard Euler/Abiturvorbereitung mit hilfreichen Links: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
(Abiaufgabe_1)
 
 
(15 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
 +
[http://www.abiturloesung.de/|Abituraufgaben mit Lösungen]
 +
[http://www.serlo.org/math/wiki/article/view/e-funktion|e-Funktion Veranschaulichung] <br /><br />
 
'''Abituraufgabe 2012 - Infinitesimalrechnung '''
 
'''Abituraufgabe 2012 - Infinitesimalrechnung '''
 
<br />
 
<br />
Zeile 8: Zeile 10:
 
Geben Sie das Verhalten von g für  x <math>\rightarrow</math> - <math>\infty</math> und x <math>\rightarrow</math> + <math>\infty</math> an.
 
Geben Sie das Verhalten von g für  x <math>\rightarrow</math> - <math>\infty</math> und x <math>\rightarrow</math> + <math>\infty</math> an.
 
<br /><br /><br />
 
<br /><br /><br />
−
<popup name="Lösung">
+
 
 +
<div style="float:left"><popup name="Lösung Teilaufgabe 1 2a">
 +
<br /> '''Teilaufgabe 1 2a''' <br />
 
1. Ableitung bilden: g(x) = x<math>\cdot</math>e<sup>-2x</sup>
 
1. Ableitung bilden: g(x) = x<math>\cdot</math>e<sup>-2x</sup>
 
<br /> ''Produktregel:'' <br />
 
<br /> ''Produktregel:'' <br />
 
g'(x) = 1 <math>\cdot</math> e<sup>-2x</sup> + x<math>\cdot</math>(-2)<math>\cdot</math>e<sup>-2x</sup> ; <br />
 
g'(x) = 1 <math>\cdot</math> e<sup>-2x</sup> + x<math>\cdot</math>(-2)<math>\cdot</math>e<sup>-2x</sup> ; <br />
 
g'(x) = e<sup>-2x</sup> <math>\cdot</math>(1+(-2x); <br />
 
g'(x) = e<sup>-2x</sup> <math>\cdot</math>(1+(-2x); <br />
−
g'(x) = e<sup>-2x</sup> <math>\cdot</math> (1-2x);
+
g'(x) = e<sup>-2x</sup> <math>\cdot</math> (1-2x);<br />
−
</popup>
+
<br /> 2. Nullstellen der Ableitung bestimmen (Extremwerte der Funktion g(x))<br />
 +
e<sup>-2x</sup> ist immer größer 0. ''Daher:'' <br />
 +
1-2x = 0;  2x = 1;  '''x = 0,5;''' <br /><br />
 +
3. Koordinaten des Punktes der waagrechten Tangente bestimmen. <br />
 +
g(0,5) = 0,5 <math>\cdot</math> e<sup>-2 <math>\cdot</math> 0,5</sup>;
 +
<br />  g(0,5)= <math>\frac 1 {2e}</math>
 +
<br /><br /> '''P(0,5/ <math>\frac 1 {2e}</math>);'''
 +
<br />
 +
</popup></div>
 +
<div style="float:left"><popup name="Lösung Teilaufgabe 1 2b">
 +
<br />'''Teilaufgabe 1 2b''' <br />
 +
Grenzwerte bilden: g(x) = x<math>\cdot</math>e<sup>-2x</sup>
 +
<br /> - Grenzwert x <math>\rightarrow</math> - <math>\infty</math>:    '''lim g(x)= - <math>\infty</math>;'''
 +
<br /> - Grenzwert x <math>\rightarrow</math> + <math>\infty</math>:    '''lim g(x)= 0;'''
 +
</popup></div>
 +
<br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br />
 +
'''Abituraufgabe 2013 - Infinitesimalrechnung '''
 +
<br />
 +
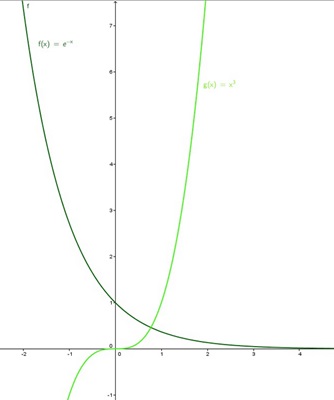
Gegeben sind die in R definierten Funktionen: g(x)=e<sup>-x</sup> und h(x)=x<sup>3</sup>;<br /><br />
 +
 
 +
''Teilaufgabe Teil 1 3a (2 BE)''<br />
 +
Veranschaulichen Sie durch eine Skizze, dass die Graphen g und h genau einen Schnittpunkt haben. <br />
 +
''Teilaufgabe Teil 1 3b (4 BE)''<br />
 +
Bestimmen Sie einen Nährungswert x<sub>1</sub> für die x-Koordinate dieses Schnittpunkts, indem Sie für die in R
 +
definierte Funktion d(x)=g(x)-h(x) den ersten Schritt des Newton-Verfahrens mit dem Startwert x<sub>0</sub>=1 durchführen.
 +
 
 +
 
 +
<div style="float:left"><popup name="Lösung Teilaufgabe 1 3a">
 +
<br /> '''Teilaufgabe 1 3a''' <br />
 +
[[Datei:Lösung_abiaufgabe_13agr.jpg]]
 +
</popup></div>
 +
<div style="float:left"><popup name="Lösung Teilaufgabe 1 3b">
 +
<br />'''Teilaufgabe 1 3b''' <br />
 +
Newtonsche Iterationsformel zur näherungsweisen Berechnung von Nullstellen. <br />
 +
x<sub>0</sub> = 1; →Startwert <br />
 +
x<sub>n+1</sub> = x<sub>n</sub> - <math>\frac {e^{-x} -x^3} {-e^x - 3x</math> = <br /><br />
 +
= 1 - <math>\frac {e^{-1} - 1^3} {-e^{-1} - 3 = <br /> <br />
 +
= 0{,}812
 +
</popup></div>
 +
 
 +
 
 +
 
 +
<br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br />
 +
 
 +
<div style="float:left"><div style="border: 1px solid #808000; background-color:#808000; font-size:1px; height:8px; border-bottom:1px solid #808000;"></div>
 +
<div style="border: 1px solid #808000; background-color:#F5F5DC; padding:30px;">
 +
[[Leonhard Euler/Kurzbiographie|Kurzbiographie]]
 +
</div> </div>
 +
<div style="float:left"><div style="border: 1px solid #808000; background-color:#808000; font-size:1px; height:8px; border-bottom:1px solid #808000;"></div>
 +
<div style="border: 1px solid #808000; background-color:#F5F5DC; padding:30px;">
 +
[[Leonhard Euler/Wissenswertes|Wissenswertes]]
 +
</div> </div>
 +
<div style="float:left"><div style="border: 1px solid #808000; background-color:#808000; font-size:1px; height:8px; border-bottom:1px solid #808000;"></div>
 +
<div style="border: 1px solid #808000; background-color:#F5F5DC; padding:30px;">
 +
[[Leonhard Euler/Thema der Seminararbeit|Thema der Seminararbeit]]
 +
</div> </div>
 +
<div style="float:left"><div style="border: 1px solid #808000; background-color:#808000; font-size:1px; height:8px; border-bottom:1px solid #808000;"></div>
 +
<div style="border: 1px solid #808000; background-color:#F5F5DC; padding:30px;">
 +
[[Leonhard Euler/Quellen|Quellen]]
 +
</div> </div>
 +
<div style="float:left"><div style="border: 1px solid #808000; background-color:#808000; font-size:1px; height:8px; border-bottom:1px solid #808000;"></div>
 +
<div style="border: 1px solid #808000; background-color:#F5F5DC; padding:30px;">
 +
[[Leonhard Euler/Einstiegsaufgaben|Einstiegsaufgaben]]
 +
</div> </div>
 +
<div style="float:left"><div style="border: 1px solid #808000; background-color:#808000; font-size:1px; height:8px; border-bottom:1px solid #808000;"></div>
 +
<div style="border: 1px solid #808000; background-color:#F5F5DC; padding:30px;">
 +
[[Leonhard Euler/Weiterführende Aufgaben|Weiterführende Aufgaben]]
 +
</div> </div>
 +
<div style="float:left"><div style="border: 1px solid #808000; background-color:#808000; font-size:1px; height:8px; border-bottom:1px solid #808000;"></div>
 +
<div style="border: 1px solid #808000; background-color:#ABC; padding:30px;">
 +
[[Leonhard Euler/Abiturvorbereitung mit hilfreichen Links|Abiturvorbereitung mit hilfreichen Links]]
 +
</div> </div>
 +
<div style="float:left"><div style="border: 1px solid #808000; background-color:#808000; font-size:1px; height:8px; border-bottom:1px solid #808000;"></div>
 +
<div style="border: 1px solid #808000; background-color:#F5F5DC; padding:30px;">
 +
[[Benutzer: Renner Lisa|Startseite]]
 +
</div> </div>

Aktuelle Version vom 4. November 2013, 19:58 Uhr

mit Lösungen Veranschaulichung

Abituraufgabe 2012 - Infinitesimalrechnung
Gegeben ist die in R definierte Funktion g(x) = x\cdote-2x.

Teilaufgabe Teil 1 2a (5 BE)
Bestimmen Sie die Koordinaten des Punkts, in dem der Graph von g eine waagrechte Tangente hat.
Teilaufgabe Teil 1 2b (2 BE)
Geben Sie das Verhalten von g für  x \rightarrow - \infty und x \rightarrow + \infty an.

























Abituraufgabe 2013 - Infinitesimalrechnung
Gegeben sind die in R definierten Funktionen: g(x)=e-x und h(x)=x3;

Teilaufgabe Teil 1 3a (2 BE)
Veranschaulichen Sie durch eine Skizze, dass die Graphen g und h genau einen Schnittpunkt haben.
Teilaufgabe Teil 1 3b (4 BE)
Bestimmen Sie einen Nährungswert x1 für die x-Koordinate dieses Schnittpunkts, indem Sie für die in R definierte Funktion d(x)=g(x)-h(x) den ersten Schritt des Newton-Verfahrens mit dem Startwert x0=1 durchführen.


































Kurzbiographie

Wissenswertes

Thema der Seminararbeit

Quellen

Einstiegsaufgaben

Weiterführende Aufgaben

Abiturvorbereitung mit hilfreichen Links

Startseite

Von „http://rmg.zum.de/index.php?title=Leonhard_Euler/Abiturvorbereitung_mit_hilfreichen_Links&oldid=54512“