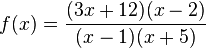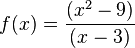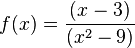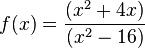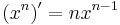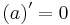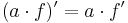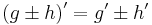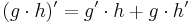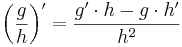Q11 Mathematik: Unterschied zwischen den Versionen
Aus RMG-Wiki
(→12. Modellieren) |
|||
| (3 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 23: | Zeile 23: | ||
===Kurse=== | ===Kurse=== | ||
| + | 2018/2020: [[Q11 Mathematik/M1 2018_20|M1 OBL]] | ||
| + | |||
2016/2018: [[Q11 Mathematik/M1 2016_18|M1 EIR]] - [[Q11 Mathematik/M3 2016_18|M3 HET]] - [[Q11 Mathematik/M6 2016_18|M6 OBL]] - [[Q11 Mathematik/AufgabenübersichtKlausur1|Aufgabenübersicht 1.Klausur (EIR,HET,SHE) ]] - [[Q11 Mathematik/M2 2016_18|M2 GRAE]] | 2016/2018: [[Q11 Mathematik/M1 2016_18|M1 EIR]] - [[Q11 Mathematik/M3 2016_18|M3 HET]] - [[Q11 Mathematik/M6 2016_18|M6 OBL]] - [[Q11 Mathematik/AufgabenübersichtKlausur1|Aufgabenübersicht 1.Klausur (EIR,HET,SHE) ]] - [[Q11 Mathematik/M2 2016_18|M2 GRAE]] | ||
| Zeile 242: | Zeile 244: | ||
#[[Media:Verknüpfen von Ereignissen.doc|Verknüpfen von Ereignissen]] | #[[Media:Verknüpfen von Ereignissen.doc|Verknüpfen von Ereignissen]] | ||
#[[Media:Unabhängigkeit.doc|Unabhängigkeit]] | #[[Media:Unabhängigkeit.doc|Unabhängigkeit]] | ||
| − | #Lösungen Buch: [[Q11 Mathematik/Seite185| | + | #Lösungen Buch: [[Q11 Mathematik/Seite185|185ff]] |
</td></tr></table></center> | </td></tr></table></center> | ||
</div> | </div> | ||
| Zeile 253: | Zeile 255: | ||
====12. Modellieren==== | ====12. Modellieren==== | ||
| − | [[ | + | #[[Q11 Mathematik/Lösung Abituraufgabe 2016 Analysis II|Lösung Abituraufgabe 2016 Analysis II]] |
| + | |||
</td></tr></table></center> | </td></tr></table></center> | ||
Aktuelle Version vom 15. Mai 2019, 16:57 Uhr
Allgemeine Informationen
(Inhalte sind Ergebnisse einer Gruppenarbeit im Unterricht. Keine Garantie bzgl. Vollständigkeit und Fehlerfreiheit.) Kurse2018/2020: M1 OBL 2016/2018: M1 EIR - M3 HET - M6 OBL - Aufgabenübersicht 1.Klausur (EIR,HET,SHE) - M2 GRAE 2015/2017: M5 EIR - M5 SHE - M8 HET - M3 BEK 2014/2016: M8 BEK |
1. Gebrochenrationale FunktionenLösungen Buch: Lösungen AH: Graphen einfacher gebrochenrationaler Funktionen Videos: Kurvendiskussion zu den Funktionen (englisch) |
2. Differenzenquotient - mittlere Änderungsrate -Steigung Sekante |
3. Differentialquotient - lokale Änderungsrate - Steigung Tangente
|
4. Ableitungsfunktion |
5. Ableitungsregeln
|
6. Monotonie, Extrema, Funktionsuntersuchung
|
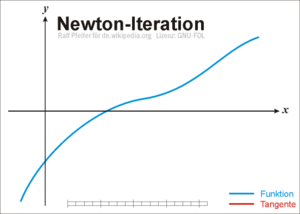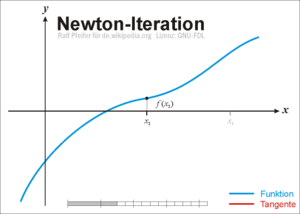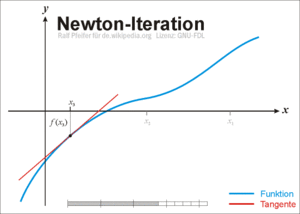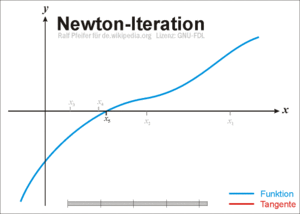
7. Newton-Verfahren
|
8. Analytische Geometrie
|
9. Weitere Ableitungsregeln
|
11. Wahrscheinlichkeitsbegriff und Unabhängigkeit
|
12. Modellieren
|
14. Funktionen mit Parametern
|
15. Kurvendiskussion |
16. Abituraufgaben |