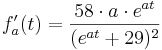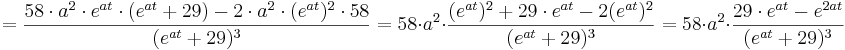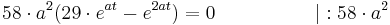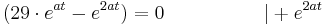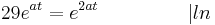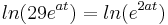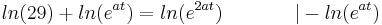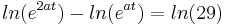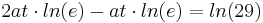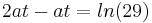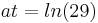Lösung b): Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
(→‎Jeder Graph Ga bestitzt genau einen Wendepunkt Wa. Zeigen sie, dass die Wendepunkte Wa auf einer parallelen zur t-Achse liegen)
(→‎Jeder Graph Ga bestitzt genau einen Wendepunkt Wa. Zeigen sie, dass die Wendepunkte Wa auf einer parallelen zur t-Achse liegen)
Zeile 48: Zeile 48:
 
'''1. Möglichkeit: Vorzeichentabelle'''
 
'''1. Möglichkeit: Vorzeichentabelle'''
  
−
Die Möglichkeit des Nachweises durch die Vorzeichentabelle, ist eine vereinfachte Form der [[H-Methode. Sie ist deutlich zeitsparender, weshalb sie von mir in Prüfungen empfohlen wird, da somit sehr schnell und fehlerfrei nachgewiesen werden kann, ob es einen Vorzeichenwechsel an der möglichen Stelle gibt.
+
Die Möglichkeit des Nachweises durch die Vorzeichentabelle, ist eine vereinfachte Form der [[Facharbeit Mathematik Straßheimer/Die Aufgabe/Lösung b)/Weitere Verfahren/H-Methode|H-Methode]]. Sie ist deutlich zeitsparender, weshalb sie von mir in Prüfungen empfohlen wird, da somit sehr schnell und fehlerfrei nachgewiesen werden kann, ob es einen Vorzeichenwechsel an der möglichen Stelle gibt.
  
 
Man zerlegt die 2. Ableitung in seine einzelnen Faktoren und betrachtet das Verhalten vor dem möglichen Wendepunkt und nach dem möglichen Wendepunkt. Man notiert sich nun, ob es einen Vorzeichenwechsel bei einem der Faktoren gibt und schlussfolgert aus den einzelnen Vorzeichenwechsel den Vorzeichenwechsel der 2. Ableitung.<br />
 
Man zerlegt die 2. Ableitung in seine einzelnen Faktoren und betrachtet das Verhalten vor dem möglichen Wendepunkt und nach dem möglichen Wendepunkt. Man notiert sich nun, ob es einen Vorzeichenwechsel bei einem der Faktoren gibt und schlussfolgert aus den einzelnen Vorzeichenwechsel den Vorzeichenwechsel der 2. Ableitung.<br />
Zeile 55: Zeile 55:
 
Aus der Vorzeichentabelle lässt sich nun ganz leicht erkennen, dass es an der Stelle <math>\frac {ln29}{a}</math> einen Vorzeichenwechsel der 2. Ableitung von <math>+</math> zu <math>-</math> gibt. Somit ist es ein Beweis für einen Wendepunkt.
 
Aus der Vorzeichentabelle lässt sich nun ganz leicht erkennen, dass es an der Stelle <math>\frac {ln29}{a}</math> einen Vorzeichenwechsel der 2. Ableitung von <math>+</math> zu <math>-</math> gibt. Somit ist es ein Beweis für einen Wendepunkt.
  
−
Es gibt noch 2 weitere Beweisverfahren, welche mathematisch gesehen etwas korrekter sind, allerdings für eine Prüfung wie das Abitur nicht zu empfehlen sind. Falls jemand diese Beweisverfahren sehen möchte, bitte hier klicken.
+
Es gibt noch 2 weitere Beweisverfahren, welche mathematisch gesehen etwas korrekter sind, allerdings für eine Prüfung wie das Abitur nicht zu empfehlen sind. Falls jemand diese Beweisverfahren sehen möchte, bitte [[Facharbeit Mathematik Straßheimer/Die Aufgabe/Lösung b)/Weitere Verfahren|hier]] klicken.<br />
 +
 
 
'''<u>Begründung, warum alle Wendepunkte auf einer Parallelen zur t-Achse liegen:</u>'''
 
'''<u>Begründung, warum alle Wendepunkte auf einer Parallelen zur t-Achse liegen:</u>'''
  

Version vom 26. Januar 2010, 13:43 Uhr

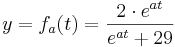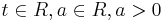
y = f_{a}(t) = \frac{2\cdot e^{at}}{e^{at}+29}, t\in R, a\in R, a>0
f'_{a} (t) = \frac{58\cdot a\cdot e^{at} }{(e^{at}+29) ^{2}}

Untersuchen sie die Funktionen fa auf Nullstellen und lokale Extremstellen

Suche nach Nullstellen:

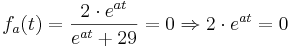
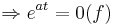
f_{a}(t) = \frac{2\cdot e^{at}}{e^{at}+29} = 0 \Rightarrow 2\cdot e^{at} = 0 \Rightarrow e^{at} = 0 (f)

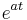\Rightarrow keine Nullstellen, da die e-Funktion nie 0 wird und somit der Ausdruck e^{at}\; ebenfalls nie 0 werden kann

Suche nach Extremstellen:

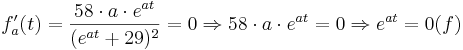
f'_{a} (t) = \frac{58\cdot a\cdot e^{at} }{(e^{at}+29) ^{2}} = 0 \Rightarrow 58\cdot a \cdot e^{at} = 0 \Rightarrow e^{at} = 0 (f)

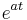\Rightarrow keine Extremstellen, da die e-Funktion nie 0 wird und somit der Ausdruck e^{at}\; ebenfalls nie 0 werden kann

Jeder Graph Ga bestitzt genau einen Wendepunkt Wa. Zeigen sie, dass die Wendepunkte Wa auf einer parallelen zur t-Achse liegen

Die 2. Ableitung:

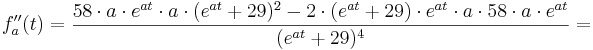
f''_{a}(t) = \frac{58\cdot a \cdot e^{at}\cdot a\cdot(e^{at}+29)^{2} - 2 \cdot(e^{at} + 29)\cdot e^{at}\cdot a \cdot 58 \cdot a \cdot e^{at} }{(e^{at} + 29) ^{4} } =

= \frac{58\cdot a^{2} \cdot e^{at}\cdot (e^{at} + 29) - 2\cdot a^{2} \cdot (e^{at})^{2}\cdot 58 }{(e^{at}+29)^{3}} = 58\cdot a^{2}\cdot \frac{(e^{at})^{2} + 29\cdot e^{at} - 2(e^{at})^2}{(e^{at} + 29)^{3}} = 58\cdot a^{2} \cdot \frac {29\cdot e^{at} - e^{2at}}{(e^{at}+29)^{3}}

Suche nach dem Wendepunkt:

Um den Wendepunkt zu finden, muss man die 2. Ableitung gleich 0 setzen. Die x-Koordinate, die man als mögliches Ergebnis bekommt, ist die Stelle, an der ein Wendepunkt auftreten kann.

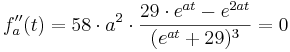
f''_{a}(t) = 58\cdot a^{2} \cdot \frac {29\cdot e^{at} - e^{2at}}{(e^{at}+29)^{3}} = 0

58\cdot a^{2} (29\cdot e^{at} - e^{2at}) = 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;| : 58\cdot a^{2}
(29\cdot e^{at} - e^{2at}) = 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;| + e^{2at}\;
29 e^{at} = e^{2at}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;| ln\;
ln(29 e^{at}) = ln(e^{2at})\;
ln(29) + ln(e^{at}) = ln(e^{2at})\;\;\;\;\;\;\;\;\;\;\;\;\;| - ln(e^{at})\;
ln(e^{2at}) - ln(e^{at}) = ln(29)\;
2at \cdot ln(e) - at\cdot ln(e) = ln(29)
2at - at = ln(29)\;
at = ln(29)\;
t = \frac {ln29} {a}

Daraus folgt, dass es an der Stelle 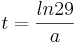t = \frac {ln29} {a} einen Wendepunkt geben kann. Dies muss allerdings noch weiter überprüft und bewiesen werden.

Beweis für Wendepunkt:


1. Möglichkeit: Vorzeichentabelle

Die Möglichkeit des Nachweises durch die Vorzeichentabelle, ist eine vereinfachte Form der H-Methode. Sie ist deutlich zeitsparender, weshalb sie von mir in Prüfungen empfohlen wird, da somit sehr schnell und fehlerfrei nachgewiesen werden kann, ob es einen Vorzeichenwechsel an der möglichen Stelle gibt.

Man zerlegt die 2. Ableitung in seine einzelnen Faktoren und betrachtet das Verhalten vor dem möglichen Wendepunkt und nach dem möglichen Wendepunkt. Man notiert sich nun, ob es einen Vorzeichenwechsel bei einem der Faktoren gibt und schlussfolgert aus den einzelnen Vorzeichenwechsel den Vorzeichenwechsel der 2. Ableitung.
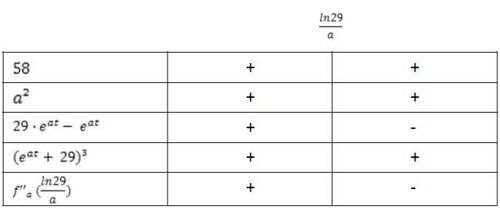
Vorzeichentabelle Facharbeit2.jpg

Aus der Vorzeichentabelle lässt sich nun ganz leicht erkennen, dass es an der Stelle 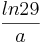\frac {ln29}{a} einen Vorzeichenwechsel der 2. Ableitung von 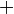+ zu - gibt. Somit ist es ein Beweis für einen Wendepunkt.

Es gibt noch 2 weitere Beweisverfahren, welche mathematisch gesehen etwas korrekter sind, allerdings für eine Prüfung wie das Abitur nicht zu empfehlen sind. Falls jemand diese Beweisverfahren sehen möchte, bitte hier klicken.

Begründung, warum alle Wendepunkte auf einer Parallelen zur t-Achse liegen:

Da wir nun zweifelsfrei nachgewiesen haben, dass es einen Wendepunkt an der Stelle 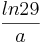\frac {ln29}{a} gibt, muss nun gezeigt werden, dass alle diese Wendepunkte auf einer Parallelen zur t-Achse liegen.

Bedingung: Alle y-Werte müssen gleich sein

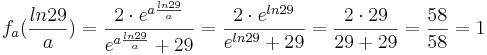
f_{a} (\frac {ln29}{a}) = \frac {2\cdot e^{a\frac {ln29}{a}}} {e^{a\frac {ln29}{a}} + 29} = \frac {2\cdot e^{ln29}} {e^{ln29} + 29} = \frac {2\cdot 29} {29 + 29} = \frac {58}{58} = 1

An dem y-Wert sieht man, dass jeder Wendepunkt den y-Wert 1 hat und dieser völlig unabhängig von a ist. Somit ist zweifelsfrei nachgewiesen worden, dass alle Wendepunkte auf einer Parallelen zur t-Achse liegen

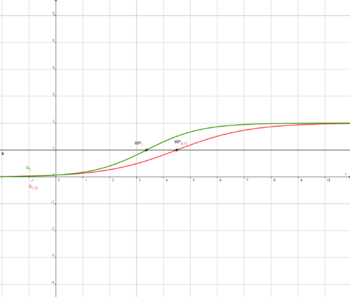
Zeichnen sie die Graphen G0,75 und G1 in ein und dasselbe Koordinatensystem und schlussfolgern Sie, welchen Einfluss der Parameter a auf den Verlauf der Graphen Ga hat

Der Graph der Funktion

Man soll nun die beiden Graphen G1 und G0,75 miteinander vergleichen. Im nebenstehenden Bild kann man die Graphen, sowie die beiden Wendepunkte und die Ortskurve der Wendepunkte erkennen. Der rote Graph beschreibt die Funktion f_{0,75} (t)\; und der grüne die Funktion f_{1} (t)\;.

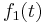Anhand der Graphen lässt sich nun sehr leicht der Einfluss der Variablen a auf den Graphen der Funktion festmachen. Wie man erkennen kann, ist die Variable a für die Steigung des Graphen verantwortlich. Je größer a wird, desto größer ist die Steigung im Wendepunkt WPa. Außerdem verlagert sich die x-Koordinate, des Wendepunkts immer weiter nach "links", was bedeutet, dass sie immer kleiner wird.

Für diejenigen, die den allgemeinen Verlauf in Abhängigkeit von a nochmals sehen wollen

Von „http://rmg.zum.de/index.php?title=Facharbeit_Mathematik_Straßheimer/Die_Aufgabe/Lösung_b)&oldid=28135“