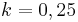Lernpfad zur zentrischen Streckung und den Ähnlichkeitssätzen/Zentrische Streckung - Übung 2
Aus RMG-Wiki
Löse folgende Aufgaben in deinem Heft.
Aufgabe 1
Aufgabe:
Aufgabe 2
Aufgabe:
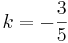 .
.Aufgabe 3
Aufgabe:
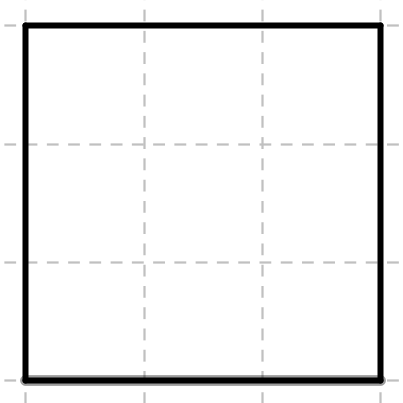
Das Quadrat ABCD soll zentrisch gestreckt werden. Streckzentrum ist der Punkt C und der Streckfaktor ist k = 0,25.

 Punkt und Bildpunkt liegen von A aus gesehen in entgegengesetzter Richtung.
Punkt und Bildpunkt liegen von A aus gesehen in entgegengesetzter Richtung.
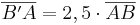
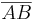 anträgst.
anträgst.
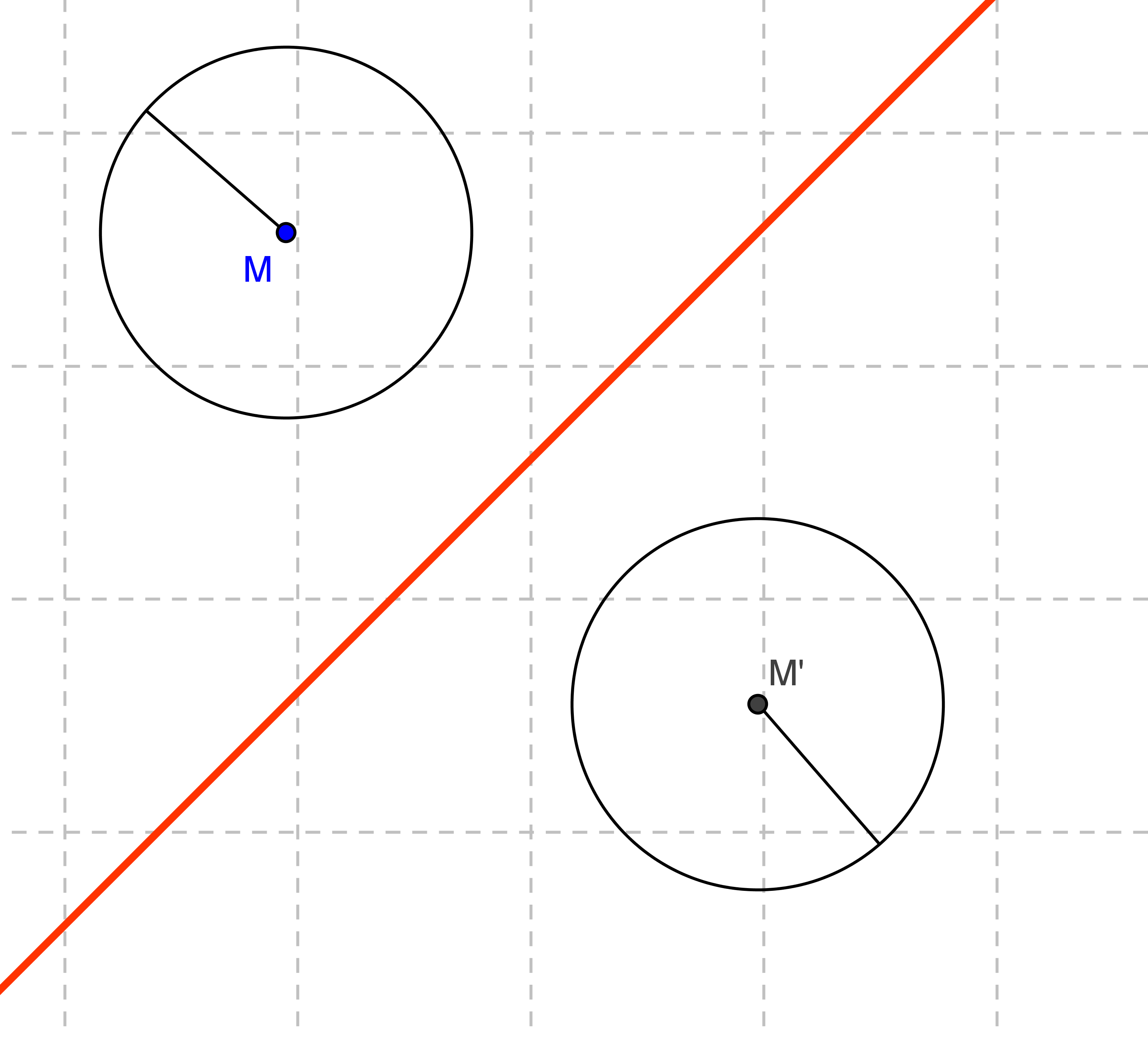
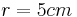 und dem Mittelpunkt M.
und dem Mittelpunkt M.
 k)
k)