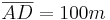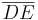Lernpfad zur zentrischen Streckung und den Ähnlichkeitssätzen/Zentrische Streckung - Übung 1
Löse die folgenden Übungsaufgaben in deinem Heft.
Aufgabe 1
Aufgabe:
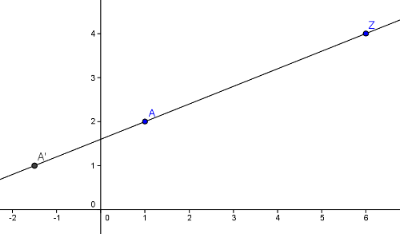
Der Punkt A(1/2) soll am Punkt Z(6/4) um den Faktor k = 1,5 zentrisch gestreckt werden.
- Z ist das Streckzentrum
- Der Streckfaktor ist
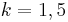
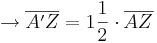
 Du musst an die Halbgerade [ZA eineinhalb mal
Du musst an die Halbgerade [ZA eineinhalb mal 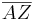 antragen.
antragen.
Aufgabe 2
|
Aufgabe: |
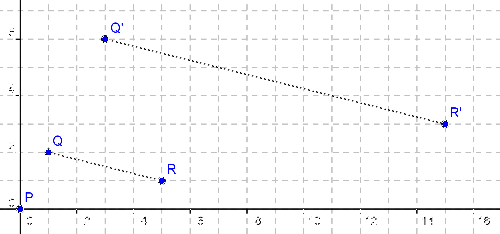
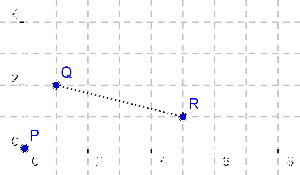
Um die Bildstrecke [Q'R'] zu erhalten musst du durch Zentrische Streckung die Bildpunkte Q' und R' ermitteln und sie verbinden.
 Q'(3/6); R'(15/3)
Q'(3/6); R'(15/3)
Aufgabe 3
|
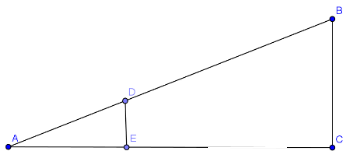
Aufgabe: Berechne den Höhenunterschied in deinem Heft. |
Wenn du noch keine Idee hast, dann kannst du hier eine Skizze ansehen.
Hier noch ein weiterer Tip
- Die Gerade [AB] bekommt man durch eine Zentrische Streckung der Geraden [AD] am Streckzentrum A.
- Die Gerade [BC] geht aus einer Zentrischen Streckung von [DE] an A hervor.
Und hier die komplette Lösung
- Berechnung des Streckfaktors k:
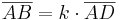
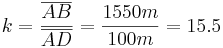
- Berechnung des Höhenunterschiedes:
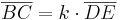
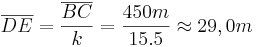
Der durchschnittliche Höhenunterschied, der auf 100m überwunden wird, beträgt 29m.

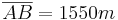 ;
;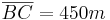 ;
;