- Aufgabe 2
|
|
|
|
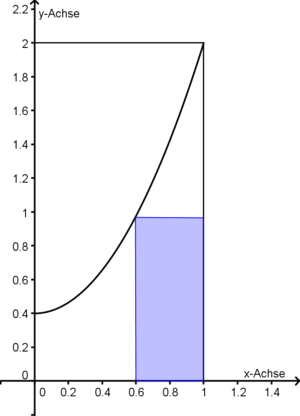
Aus rechteckigen Kunststoffplatten von 1 Meter Breite und 2 Meter Höhe wurden Stücke abgeschnitten, wobei die Schnittkurve pt Teil einer Parabel ist, die der Gleichung y=tx2+2-t genügt. Für den Parameter t gilt: 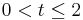 . In nebenstehender Skizze ist der Fall t=1,6 dargestellt. . In nebenstehender Skizze ist der Fall t=1,6 dargestellt.
|
|
|
- a) Zeigen Sie, dass jede Schnittkurve pt durch den Punkt (1/2) verläuft. Beschreiben Sie die Bewegung des Parabelscheitels, wenn t bei 2 beginnend alle Werte des Intervalls ]0;2] durchläuft.
- [Lösung anzeigen][Lösung ausblenden]
Bemerkung:
In der 2ten Zeile wurde für t 1 eingesetzt. Allerdings muss hier t stehen bleiben, nur für x wird 1 eingesetzt.-> ERLEDIGT

3 BE
- Aus der Restplatte werden Rechtecke – wie in der Skizze schraffiert (markiert) dargestellt – ausgeschnitten. Je eine Seite des Rechtecks soll auf dem unteren bzw. auf dem rechten Rand der Platte zu liegen kommen, eine Ecke des Rechtecks soll auf der Schnittkurve liegen.
- b) Zeigen Sie, dass für den Inhalt eines solchen Rechtecks gilt
-
- At(x)=-tx3+tx2+(t-2)x+2-t (0
 x x 1). 1).
- [Lösung anzeigen][Lösung ausblenden]
3 BE
- Der Inhalt des ausgeschnittenen Rechtecks soll möglichst groß sein (Extremwertproblem).
- c) Die unten stehende Abbildung zeigt einige Graphen der Scharfunktionen At . Beschreiben Sie, was aufgrund der Abbildung im Fall 0<t<1,5 für die Lösung des Extremwertproblems zu vermuten ist.
- Beweisen Sie Ihre Vermutung rechnerisch.
- [Lösung anzeigen][Lösung ausblenden]
6 BE
- d) Im Fall t=1,6 ist die erste Ableitung von At an den Stellen
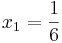 und und 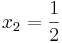 gleich Null gleich Null
- (Nachweis nicht erforderlich).
- Bestätigen Sie durch Berechnung geeigneter Werte von At , dass für t=1,6 zwei Rechtecke den maximalen Flächeninhalt aufweisen.
- [Lösung anzeigen][Lösung ausblenden]
3 BE
|