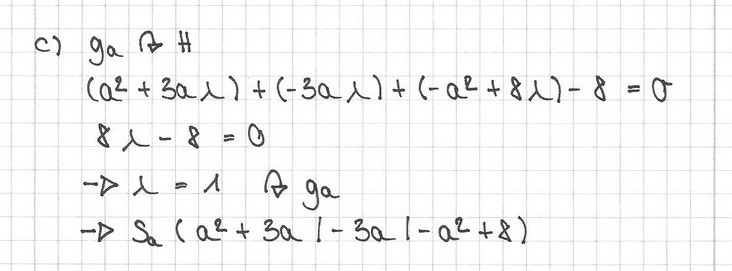- Aufgabe 1
a) Zeigen Sie, dass keine der Geraden ga parallel und keine senkrecht zur Ebene H verläuft.
3 BE
- [Lösung anzeigen][Lösung ausblenden]
b) Welche dieser Geraden schneidet H unter dem größten Winkel? Berechnen Sie diesen maximalen Winkel auf eine Dezimale genau.
6 BE
- [Lösung anzeigen][Lösung ausblenden]
c) Berechnen Sie die Koordinaten des Schnittpunkts Sa von ga mit H.
[ Zur Kontrolle: Sa = (a2 + 3a / -3a / 8 - a2) ]
3 BE
- [Lösung anzeigen][Lösung ausblenden]
d) Zeigen Sie, dass der Punkt S (-2 / 6 / 4) derjenige Punkt aus der Schar der Schnittpunkte Sa ist, der die geringste Entfernung vom Ursprung hat. Geben Sie diese Entfernung an.
9 BE
- [Lösung anzeigen][Lösung ausblenden]
e) Die Punkte Sa bilden in H eine Kurve. Diese wird parallel zur
x3-Achse in die x1x2-Ebene projiziert; die Projektion heißt P.
Fertigen Sie eine Zeichnung von P in der x1x3-Ebene an. Um welchen Kurventyp handelt es sich bei P vermutlich? Überprüfen Sie Ihre Vermutung, indem Sie eine Koordinatengleichung von P aufstellen.
8 BE
- [Lösung anzeigen][Lösung ausblenden]
|  3 ist die
Ebene H: x1 + x2 + x3 - 8 = 0 , sowie die Schar von Geraden ga :
3 ist die
Ebene H: x1 + x2 + x3 - 8 = 0 , sowie die Schar von Geraden ga : 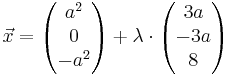 ,
, 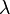 ∈
∈