Aufgabenstellung
Aus RMG-Wiki
Für jede reelle Zahl a sei eine Funktion 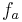 durch
durch 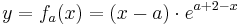 mit
mit 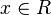 gegeben.
gegeben.
Inhaltsverzeichnis |
Teilaufgabe a)
- 1. Untersuchen Sie den Graphen von
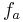 auf:
auf:
- Schnittpunkte mit den Koordinatenachsen,
- lokale Extrempunkte und
- Wendepunkte!
- Bestimmen Sie gegebenenfalls deren Koordinaten!
- 2. Alle Extrempunkte liegen auf dem Graphen einer Funktion h. Geben Sie eine Funktionsgleichung von h an!
- 3. Skizzieren Sie den Graphen der Funktion
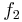 für
für 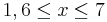 !
!
Teilaufgabe b)
- 1. Geben Sie aufgrund Ihrer Ergebnisse aus Teilaufgabe a) zwei Eigenschaften des Graphen einer Stammfunktion von
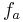 an!
an!
- 2. Bestimmen Sie durch partielle Integration eine Gleichung einer Stammfunktion von
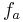 !
!
- 3. Die x-Achse und der Graph der Funktion
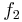 begrenzen im I. Quadranten eine nach rechts ins Unendliche reichende Fläche. Berechnen sie deren Inhalt!
begrenzen im I. Quadranten eine nach rechts ins Unendliche reichende Fläche. Berechnen sie deren Inhalt!
- Hinweis:
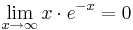
- Hinweis:
Teilaufgabe c)
- Im Punkt
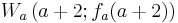 werde die Tangente an den Graphen von
werde die Tangente an den Graphen von 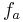 gelegt
gelegt
- 1. Für welchen Wert von a schneidet diese Tangente die y-Achse im Punkt
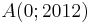 ?
?
- Nun sei
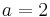 .
.
- 2. Berechnen Sie alle Stellen
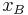 , für die die Tangente die y-Achse im Punkt
, für die die Tangente die y-Achse im Punkt 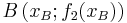 an den Graphen von
an den Graphen von 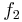 durch den Koordinatenursprung verläuft!
durch den Koordinatenursprung verläuft!
Teilaufgabe d)
Für jeden Wert von a bilden die Punkte 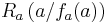 ,
, 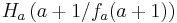 und
und 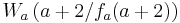 ein Dreieck.
ein Dreieck.
- 1. Zeigen Sie, dass alle diese Dreiecke zueinander kongruent sind!
- 2. Berechnen Sie deren Flächeninhalt!
Teilaufgabe e)
Beweisen Sie, dass für die n-te Ableitung (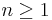 ) der Funktion
) der Funktion 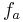 gilt:
gilt:
--Andre Etzel 22:42, 20. Jan. 2010 (UTC)