Abi 2017 Analysis II Teil B
|
|
Gegeben ist die Funktion f mit f(x) = 2e-x⋅(2e-x - 1) und x ∈ IR. a)Zeigen Sie, dass für den Term der Ableitungsfunktion f' von f gilt: f'(x) = 2e-x⋅(1-4e-x) b) Bestimmen Sie rechnerisch Lage und Art des Extrempunkts von Gf .
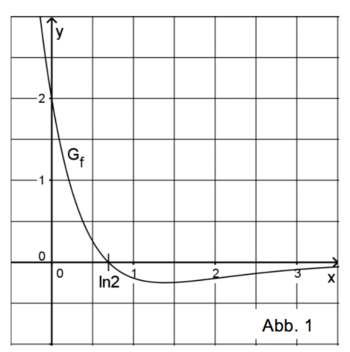
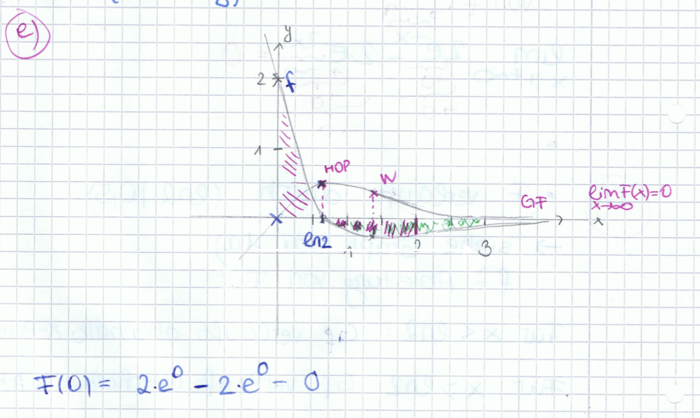
c) Zeigen Sie, dass F eine Stammfunktion von f ist, und begründen Sie anhand des Terms von F, dass d)Der Graph von F verläuft durch den Punkt (ln2|0,5). Begründen Sie ohne weitere Rechnung, dass F keine größeren Werte als 0,5 annehmen kann und bei x = ln 4 eine Wendestelle besitzt. Berechnen Sie die y-Koordinate des zugehörigen Wendepunkts. e) Zeichnen Sie den Graphen von F unter Berücksichtigung der bisherigen Ergebnisse sowie des Funktionswerts F(0) im Bereich -0,3 ≤ x ≤ 3,5 in Abbildung 1 ein. f) Der Graph von f schließt mit den Koordinatenachsen ein Flächenstück ein, das durch das Dreieck mit den Eckpunkten O(0|0), P(ln2|0) und Q (0 | 2) angenähert werden kann. Berechnen Sie, um wie viel Prozent der Flächeninhalt des Dreiecks OPQ vom Inhalt des Flächenstücks abweicht.
h)Geben Sie den Term einer in IR definierten Funktion an, die eine Stammfunktion, aber keine Integralfunktion von f ist. |
|
Zur Modellierung einer Zerfallsreihe wird vereinfachend davon ausgegangen, dass sich in einem Gefäß zu Beginn eines Beobachtungszeitraums ausschließlich der radioaktive Stoff Bi 211 befindet. Jeder Atomkern dieses Stoffs Bi 211 wandelt sich irgendwann in einen Kern des radioaktiven Stoffs Tl 207 um und dieser wiederum irgendwann in einen Kern des Stoffs Pb 207. Abbildung 2 zeigt diese Zerfallsreihe schematisch.
Für jede der drei Funktionen bezeichnet x ≥ 0 die seit Beobachtungsbeginn vergangene Zeit in der Einheit 6 Minuten. Beispielsweise bedeutet P(1)≈0,400 , dass sechs Minuten nach Beginn der Beobachtung etwa 40,0% aller Kerne im Gefäß Pb 207-Kerne sind. a) Bestimmen Sie jeweils auf zehntel Prozent genau die Anteile der drei Kernsorten zwölf Minuten nach Beobachtungsbeginn.
b) Ermitteln Sie unter Verwendung von Ergebnissen aus Aufgabe 1 den Zeitpunkt auf Sekunden genau, zu dem der Anteil von Tl 207-Kernen im Gefäß am größten ist. c) Begründen Sie rechnerisch, dass zu keinem Zeitpunkt die Anteile der drei Kernsorten gleich groß sind. d) Weisen Sie mithilfe des Terms der Funktion P nach, dass |


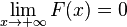 gilt.
gilt.



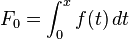 und x ∈ IR.
und x ∈ IR.





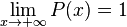 gilt, und interpretieren Sie diesen Grenzwert im Sachzusammenhang.
gilt, und interpretieren Sie diesen Grenzwert im Sachzusammenhang.


