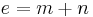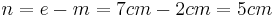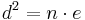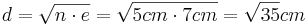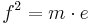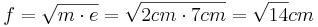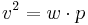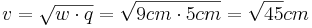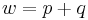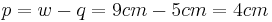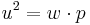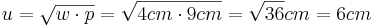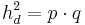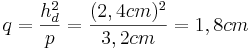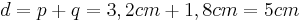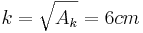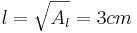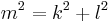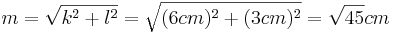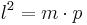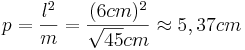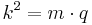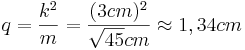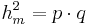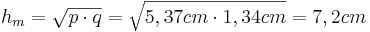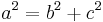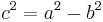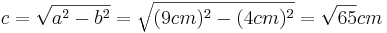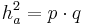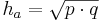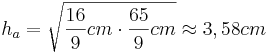Lösungen zum Übungsblatt zum Kathetensatz (Aufgaben 1-5): Unterschied zwischen den Versionen
Aus RMG-Wiki
(Internen Link und kurze Beschreibung eingefügt) |
K (Rechtschreibung verbessert) |
||
| (9 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | __NOTOC__ | |
| + | <div style="margin:0px; margin-right:90px; border:thick double green; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; "> | ||
| + | <span style="color: green">'''Arbeitsauftrag:'''</span> | ||
| + | *Hole dir das '''Übungsblatt zum Kathetensatz''' | ||
| + | *Bearbeite die Aufgaben 1-5 und vergleiche deine Lösungen mit denen auf der Seite | ||
| + | </div><br /> | ||
| − | Wenn du fertig bist geht es [[Umwandlung 1|hier]] zu einer Anwendung des Kathetensatzes | + | == Aufgabe 1== |
| + | {{Lösung versteckt| | ||
| + | *Da <math>{n\,}</math> an <math>{d\,}</math> anliegt, muss <math>{m\,}</math> an <math>{f\,}</math> anliegen<br /> | ||
| + | |||
| + | |||
| + | *<math>{e=m+n\,}</math> | ||
| + | *<math>{n=e-m=7cm-2cm=5cm\,}</math><br /> | ||
| + | |||
| + | |||
| + | *<math>d^2=n \cdot e</math> | ||
| + | *<math>d=\sqrt{n \cdot e}=\sqrt{5cm \cdot 7cm}=\sqrt{35}cm</math><br /> | ||
| + | |||
| + | |||
| + | *<math>f^2=m \cdot e</math> | ||
| + | *<math>f=\sqrt{m \cdot e}=\sqrt{2cm \cdot 7cm}=\sqrt{14}cm</math> | ||
| + | }} | ||
| + | |||
| + | == Aufgabe 2== | ||
| + | {{Lösung versteckt| | ||
| + | *<math>v^2=w \cdot p</math> | ||
| + | *<math>v=\sqrt{w \cdot q}=\sqrt{9cm \cdot 5cm}=\sqrt{45}cm</math><br /><br /> | ||
| + | |||
| + | *<math>{w=p+q\,}</math> | ||
| + | *<math>{p=w-q=9cm-5cm=4cm\,}</math><br /><br /> | ||
| + | |||
| + | *<math>u^2=w \cdot p</math> | ||
| + | *<math>u=\sqrt{w \cdot p}=\sqrt{4cm \cdot 9cm}=\sqrt{36}cm=6cm</math> | ||
| + | }} | ||
| + | |||
| + | == Aufgabe 3== | ||
| + | {{Lösung versteckt| | ||
| + | *<math>h_d^2=p \cdot q</math> | ||
| + | *<math>q=\frac{h_d^2}{p}=\frac{(2,4cm)^2}{3,2cm}=1,8cm</math><br /><br /> | ||
| + | |||
| + | *<math>{d=p+q=3,2cm+1,8cm=5cm\,}</math><br /><br /> | ||
| + | |||
| + | *<math>{c^2=h_d^2+q^2\,}</math> (Man berechnet c über den Satz des Pythagoras im kleinen rechtwinkligen Dreieck) | ||
| + | *<math>c=\sqrt{h_d^2+q^2}=\sqrt{(2,4cm)^2+(1,8cm)^2}=3cm</math><br /> | ||
| + | |||
| + | '''ODER:'''<br /> | ||
| + | |||
| + | *<math>c^2=d \cdot q</math> (Man berechnet c über den Kathetensatz im ganzen rechtwinkligen Dreieck) | ||
| + | *<math>c=\sqrt{d \cdot q}=\sqrt{5cm \cdot 1,8cm}=3cm</math><br /><br /> | ||
| + | |||
| + | *<math>{b^2=h_d^2+p^2\,}</math> (Man berechnet b über den Satz des Pythagoras im kleinen rechtwinkligen Dreieck) | ||
| + | *<math>b=\sqrt{h_d^2+p^2}=\sqrt{(2,4cm)^2+(3,2cm)^2}=4cm</math><br /> | ||
| + | |||
| + | '''ODER:'''<br /> | ||
| + | |||
| + | *<math>b^2=d \cdot p</math> (Man berechnet c über den Kathetensatz im ganzen rechtwinkligen Dreieck) | ||
| + | *<math>b=\sqrt{d \cdot p}=\sqrt{5cm \cdot 3,2cm}=4cm</math><br /><br /> | ||
| + | }} | ||
| + | |||
| + | == Aufgabe 4== | ||
| + | {{Lösung versteckt| | ||
| + | *<math>k=\sqrt{A_k}=6cm</math> | ||
| + | *<math>l=\sqrt{A_l}=3cm</math><br /><br /> | ||
| + | |||
| + | *<math>{m^2=k^2+l^2\,}</math> | ||
| + | *<math>m=\sqrt{k^2+l^2}=\sqrt{(6cm)^2+(3cm)^2}=\sqrt{45}cm</math><br /><br /> | ||
| + | |||
| + | *Wähle Hypotenusenabschnitte <math>{p\,}</math> und <math>{q\,}</math>, wobei <math>{p\,}</math> an <math>{l\,}</math> anliegt<br /> | ||
| + | |||
| + | *<math>l^2=m \cdot p</math> | ||
| + | *<math>p=\frac{l^2}{m}=\frac{(6cm)^2}{\sqrt{45}cm} \approx 5,37cm</math><br /><br /> | ||
| + | |||
| + | *<math>k^2=m \cdot q</math> | ||
| + | *<math>q=\frac{k^2}{m}=\frac{(3cm)^2}{\sqrt{45}cm} \approx 1,34cm</math><br /><br /> | ||
| + | |||
| + | *<math>h_m^2=p \cdot q</math> | ||
| + | *<math>h_m=\sqrt{p \cdot q}=\sqrt{5,37cm \cdot 1,34cm}=7,2cm</math> | ||
| + | }} | ||
| + | |||
| + | == Aufgabe 5== | ||
| + | {{Lösung versteckt| | ||
| + | *Dreieck ist rechtwinklig, da <math>180^\circ-\beta-\gamma=90^\circ</math> | ||
| + | *<math>{a\,}</math> ist Hypotenuse, da <math>{\gamma\,}</math> bei <math>{C\,}</math> liegt und <math>{\beta\,}</math> bei <math>{B\,}</math>, d.h. dem Winkel <math>{\alpha\,}</math> liegt die längste Seite, also <math>{a\,}</math> gegenüber (nicht gegeben, jedoch in der Mathematik normalerweise so gewählt)<br /><br /> | ||
| + | |||
| + | *<math>{a^2=b^2+c^2\,}</math> | ||
| + | *<math>{c^2=a^2-b^2\,}</math> | ||
| + | *<math>c=\sqrt{a^2-b^2}=\sqrt{(9cm)^2-(4cm)^2}=\sqrt{65}cm</math><br /><br /> | ||
| + | |||
| + | *Einen der beiden Hypotenusenabschnitte über den Kathetensatz berechnen: | ||
| + | *Wähle Hypotenusenabschnitte <math>{p\,}</math> anliegend an <math>{b\,}</math> und <math>{q\,}</math> anliegend an <math>{c\,}</math> | ||
| + | *<math>b^2=a \cdot p</math> | ||
| + | *<math>p=\frac{b^2}{a}=\frac{(4cm)^2}{9cm}=\frac{16}{9}cm</math><br /><br /> | ||
| + | *<math>{a=p+q\,}</math> | ||
| + | *<math>q=a-p=9cm-\frac{16}{9}cm=\frac{65}{9}cm</math><br /><br /> | ||
| + | |||
| + | *<math>h_a^2=p \cdot q</math> | ||
| + | *<math>h_a=\sqrt{p \cdot q}</math> | ||
| + | *<math>h_a=\sqrt{\frac{16}{9}cm \cdot \frac{65}{9}cm} \approx 3,58cm</math> | ||
| + | }} | ||
| + | |||
| + | |||
| + | |||
| + | Wenn du fertig bist geht es [[Lernpfad zur Satzgruppe des Pythagoras/Umwandlung Rechteck in Quadrat (K) - Seite 1|hier]] zu einer Anwendung des Kathetensatzes | ||
Aktuelle Version vom 25. Januar 2009, 20:33 Uhr
Arbeitsauftrag:
- Hole dir das Übungsblatt zum Kathetensatz
- Bearbeite die Aufgaben 1-5 und vergleiche deine Lösungen mit denen auf der Seite
Aufgabe 1
- Da
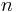 an
an 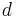 anliegt, muss
anliegt, muss 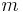 an
an 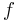 anliegen
anliegen
Aufgabe 2
Aufgabe 3
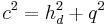 (Man berechnet c über den Satz des Pythagoras im kleinen rechtwinkligen Dreieck)
(Man berechnet c über den Satz des Pythagoras im kleinen rechtwinkligen Dreieck)
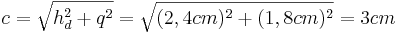
ODER:
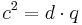 (Man berechnet c über den Kathetensatz im ganzen rechtwinkligen Dreieck)
(Man berechnet c über den Kathetensatz im ganzen rechtwinkligen Dreieck)
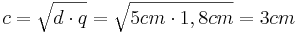
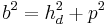 (Man berechnet b über den Satz des Pythagoras im kleinen rechtwinkligen Dreieck)
(Man berechnet b über den Satz des Pythagoras im kleinen rechtwinkligen Dreieck)
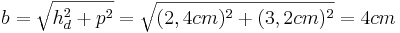
ODER:
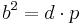 (Man berechnet c über den Kathetensatz im ganzen rechtwinkligen Dreieck)
(Man berechnet c über den Kathetensatz im ganzen rechtwinkligen Dreieck)
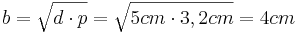
Aufgabe 4
- Wähle Hypotenusenabschnitte
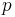 und
und 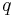 , wobei
, wobei 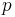 an
an 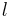 anliegt
anliegt
Aufgabe 5
- Dreieck ist rechtwinklig, da
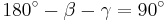
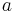 ist Hypotenuse, da
ist Hypotenuse, da 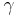 bei
bei 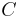 liegt und
liegt und 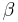 bei
bei 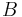 , d.h. dem Winkel
, d.h. dem Winkel 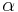 liegt die längste Seite, also
liegt die längste Seite, also 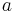 gegenüber (nicht gegeben, jedoch in der Mathematik normalerweise so gewählt)
gegenüber (nicht gegeben, jedoch in der Mathematik normalerweise so gewählt)
- Einen der beiden Hypotenusenabschnitte über den Kathetensatz berechnen:
- Wähle Hypotenusenabschnitte
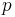 anliegend an
anliegend an 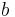 und
und 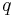 anliegend an
anliegend an 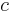
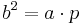
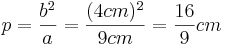
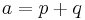
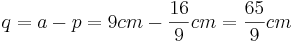
Wenn du fertig bist geht es hier zu einer Anwendung des Kathetensatzes