Lösungen für das Übungsblatt zum Höhensatz (Aufgaben 1-6): Unterschied zwischen den Versionen
Aus RMG-Wiki
K (Fehler in Formel verbessert) |
K (Rechtschreibung verbessert) |
||
| Zeile 26: | Zeile 26: | ||
*<math>h_g \approx 3,47cm</math><br /><br /> | *<math>h_g \approx 3,47cm</math><br /><br /> | ||
*Da man nun die Hypotenuse und die Höhe kennt kann man den Flächeninhalt des Dreiecks berechnen | *Da man nun die Hypotenuse und die Höhe kennt kann man den Flächeninhalt des Dreiecks berechnen | ||
| − | *<math>A_D=\frac{1}{2} \cdot | + | *<math>A_D=\frac{1}{2} \cdot g \cdot h</math> |
*<math>A_D=\frac{1}{2} \cdot g \cdot h_g</math> | *<math>A_D=\frac{1}{2} \cdot g \cdot h_g</math> | ||
*<math>A_D=\frac{1}{2} \cdot 8,06cm \cdot 3,47cm</math> | *<math>A_D=\frac{1}{2} \cdot 8,06cm \cdot 3,47cm</math> | ||
| Zeile 61: | Zeile 61: | ||
{{Lösung versteckt| | {{Lösung versteckt| | ||
*Die Höhe teilt das rechtwinklige Dreieck in zwei kleinere rechtwinklige Dreiecke | *Die Höhe teilt das rechtwinklige Dreieck in zwei kleinere rechtwinklige Dreiecke | ||
| − | *Man kann über den Satz des Pythagoras die Länge | + | *Man kann über den Satz des Pythagoras die Länge einer der beiden Hypotenusenabschnitte ausrechnen |
*Wähle <math>{Hypotenusenabschnitt_1=x\,}</math> | *Wähle <math>{Hypotenusenabschnitt_1=x\,}</math> | ||
*<math>{c^2=x^2+h_b^2\,}</math> | *<math>{c^2=x^2+h_b^2\,}</math> | ||
| Zeile 85: | Zeile 85: | ||
{{Lösung versteckt| | {{Lösung versteckt| | ||
*Bei dem gegebenen Dreieck handelt es sich um ein gleichschenkliges Dreieck | *Bei dem gegebenen Dreieck handelt es sich um ein gleichschenkliges Dreieck | ||
| − | *Die Höhe in einem gleichschenkligen Dreieck auf die Basis teilt diese in zwei | + | *Die Höhe in einem gleichschenkligen Dreieck auf die Basis teilt diese in zwei gleichgroße Teile |
*Im gegebenen Dreieck ist die Hypotenuse die Basis, da die Katheten gleich lang sind und damit die Schenkel sein müssen | *Im gegebenen Dreieck ist die Hypotenuse die Basis, da die Katheten gleich lang sind und damit die Schenkel sein müssen | ||
*Man kann die Länge der Hypotenuse über den Satz des Pythagoras berechnen | *Man kann die Länge der Hypotenuse über den Satz des Pythagoras berechnen | ||
| Zeile 92: | Zeile 92: | ||
*<math>a=\sqrt{(4cm)^2+(4cm)^2}=\sqrt{32}cm \approx 7,48cm</math><br /><br /> | *<math>a=\sqrt{(4cm)^2+(4cm)^2}=\sqrt{32}cm \approx 7,48cm</math><br /><br /> | ||
*Aufgrund der speziellen Eigenschaften in gleichschenkligen Dreiecken kann man die Länge der beiden Hypotenusenabschnitte berechnen | *Aufgrund der speziellen Eigenschaften in gleichschenkligen Dreiecken kann man die Länge der beiden Hypotenusenabschnitte berechnen | ||
| − | *Beide Hypotenusenabschnitte sind gleich und haben die halbe Länge der Hypotenuse | + | *Beide Hypotenusenabschnitte sind gleich lang und haben die halbe Länge der Hypotenuse |
*<math>Hypotenusenabschnitt_{1/2}=\frac{a}{2}</math> | *<math>Hypotenusenabschnitt_{1/2}=\frac{a}{2}</math> | ||
*<math>Hypotenusenabschnitt_{1/2}=\frac{7,48cm}{2}</math> | *<math>Hypotenusenabschnitt_{1/2}=\frac{7,48cm}{2}</math> | ||
| Zeile 100: | Zeile 100: | ||
*<math>h=\sqrt{Hypotenusenabschnitt_1 \cdot Hypotenusenabschnitt_2}</math> | *<math>h=\sqrt{Hypotenusenabschnitt_1 \cdot Hypotenusenabschnitt_2}</math> | ||
*<math>h=\sqrt{3,74cm \cdot 3,74cm}</math> | *<math>h=\sqrt{3,74cm \cdot 3,74cm}</math> | ||
| − | *<math>h=\sqrt{ | + | *<math>h=\sqrt{3,47^2}cm = 3,74cm</math> |
*<math>h=\frac{a}{2}</math> | *<math>h=\frac{a}{2}</math> | ||
}} | }} | ||
| Zeile 107: | Zeile 107: | ||
== Aufgabe 5== | == Aufgabe 5== | ||
{{Lösung versteckt| | {{Lösung versteckt| | ||
| − | *Der Abstand berechnet sich über den Satz des Pythagoras (wenn du dich nicht mehr erinnern konntest wiederhole das Kapitel entweder mit Hilfe des Lernpfades oder lies dir noch | + | *Der Abstand berechnet sich über den Satz des Pythagoras (wenn du dich nicht mehr erinnern konntest wiederhole das Kapitel entweder mit Hilfe des Lernpfades oder lies dir noch einmal deinen Hefteintrag zum Thema durch) |
*<math>d=\sqrt{(14-(-7))^2+(3-9)^2}</math> | *<math>d=\sqrt{(14-(-7))^2+(3-9)^2}</math> | ||
*<math>d=\sqrt{21^2+(-6)^2}</math> | *<math>d=\sqrt{21^2+(-6)^2}</math> | ||
| Zeile 131: | Zeile 131: | ||
c) {{Lösung versteckt| | c) {{Lösung versteckt| | ||
*Es ist ein rechtwinkliges Dreieck gegeben, also kann man die Sätze aus der Satzgruppe des Pythagoras anwenden | *Es ist ein rechtwinkliges Dreieck gegeben, also kann man die Sätze aus der Satzgruppe des Pythagoras anwenden | ||
| − | *b ist die Hypotenuse, da b die längste Seite des rechtwinkligen Dreiecks ist | + | *<math>{b\,}</math> ist die Hypotenuse, da <math>{b\,}</math> die längste Seite des rechtwinkligen Dreiecks ist |
*Damit kann man den Satz des Pythagoras ansetzen | *Damit kann man den Satz des Pythagoras ansetzen | ||
*<math>{b^2=a^2+c^2\,}</math> | *<math>{b^2=a^2+c^2\,}</math> | ||
Aktuelle Version vom 25. Januar 2009, 20:19 Uhr
Arbeitsauftrag:
- Hole dir das Übungsblatt zum Höhensatz
- Berechne die Aufgaben 1-6
- Vergleiche deine Lösungen mit denen auf der Seite
Aufgabe 1
- Im Dreieck
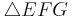 ist
ist 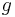 die Hypotenuse (vergleiche den Hinweis auf dem Übungsblatt)
die Hypotenuse (vergleiche den Hinweis auf dem Übungsblatt)
- Damit kann man den Satz des Pythagoras ansetzen um die Länge von
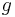 zu berechnen
zu berechnen
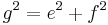
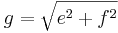
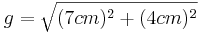
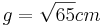
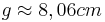
- Jetzt kann man die Länge des zweiten Hypotenusenabschnittes ausrechnen
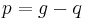
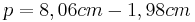
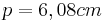
- Da man nun beide Hypotenusenabschnitte kennt kann man den Höhensatz ansetzen
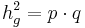
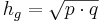
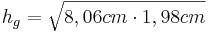
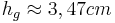
- Da man nun die Hypotenuse und die Höhe kennt kann man den Flächeninhalt des Dreiecks berechnen
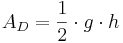
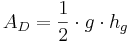
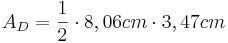
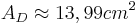
Aufgabe 2
- Da Hypotenuse (m) und ein Hypotenusenabschnitt (t) gegeben sind kann man den zweiten Hypotenusenabschnitt (x) berechnen
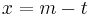
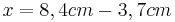
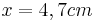
- Da jetzt die beiden Hypotenusenabschnitte bekannt sind kann man die Höhe berechnen
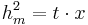
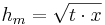
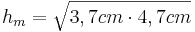
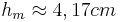
- Die Höhe teilt das rechtwinklige Dreieck in zwei kleinere rechtwinklige Dreiecke (vergleiche den Beweis zum Höhensatz)
- In jedem der beiden kleineren rechtwinkligen Dreiecke kann man die Kathete über den Satz des Pythagoras berechnen
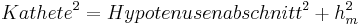
- Kathete 1
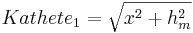
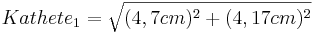
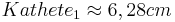
- Kathete 2
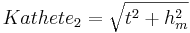
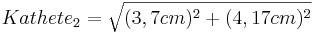
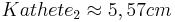
Aufgabe 3
- Die Höhe teilt das rechtwinklige Dreieck in zwei kleinere rechtwinklige Dreiecke
- Man kann über den Satz des Pythagoras die Länge einer der beiden Hypotenusenabschnitte ausrechnen
- Wähle
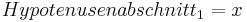
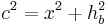
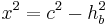
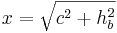
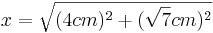
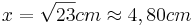
- Nun kennt man einen Hypotenusenabschnitt und die Hypotenuse
- Damit kann man den zweiten Hypotenusenabschnitt berechnen
- Wähle
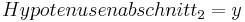
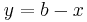
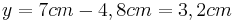
- Die Kathete d kann man über den Satz des Pythagoras berechnen
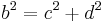
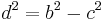
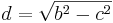
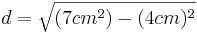
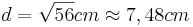
Aufgabe 4
- Bei dem gegebenen Dreieck handelt es sich um ein gleichschenkliges Dreieck
- Die Höhe in einem gleichschenkligen Dreieck auf die Basis teilt diese in zwei gleichgroße Teile
- Im gegebenen Dreieck ist die Hypotenuse die Basis, da die Katheten gleich lang sind und damit die Schenkel sein müssen
- Man kann die Länge der Hypotenuse über den Satz des Pythagoras berechnen
- Wähle
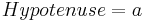
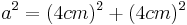
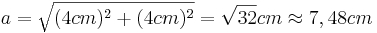
- Aufgrund der speziellen Eigenschaften in gleichschenkligen Dreiecken kann man die Länge der beiden Hypotenusenabschnitte berechnen
- Beide Hypotenusenabschnitte sind gleich lang und haben die halbe Länge der Hypotenuse
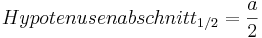
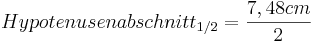
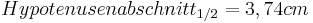
- Mit den beiden Hypotenusenabschnitten kann man nun die Höhe berechnen
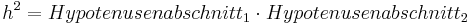
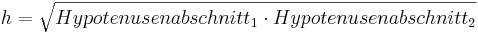
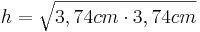
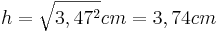
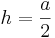
Aufgabe 5
- Der Abstand berechnet sich über den Satz des Pythagoras (wenn du dich nicht mehr erinnern konntest wiederhole das Kapitel entweder mit Hilfe des Lernpfades oder lies dir noch einmal deinen Hefteintrag zum Thema durch)
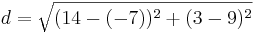
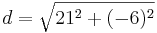
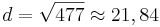
Aufgabe 6
a)
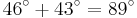 , d.h. der dritte Winkel ist nicht
, d.h. der dritte Winkel ist nicht 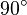 , also ist das Dreieck nicht rechtwinklig
, also ist das Dreieck nicht rechtwinklig
- Der Satz des Pythagoras kann nicht angewendet werden
b)
- Der fehlende Winkel beträgt
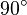 , da
, da 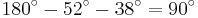
- Man kann also den Höhensatz anwenden
- Die Länge des fehlenden Hypotenusenabschnitts beträgt
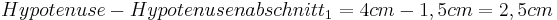
- Man kann nun die Höhe über den Höhensatz berechnen
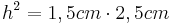
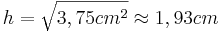
c)
- Es ist ein rechtwinkliges Dreieck gegeben, also kann man die Sätze aus der Satzgruppe des Pythagoras anwenden
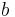 ist die Hypotenuse, da
ist die Hypotenuse, da 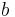 die längste Seite des rechtwinkligen Dreiecks ist
die längste Seite des rechtwinkligen Dreiecks ist
- Damit kann man den Satz des Pythagoras ansetzen
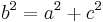
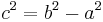
Wenn du fertig bist geht es hier zu einer Anwendung des Höhensatzes

