Verfahren Extremwertbeweis durch 2. Ableitung
Extremwertbeweis durch die 2. Ableitung:
Ein Extremwertbeweis ist neben den beiden anderen genannten Möglichkeiten ebenfalls mit Hilfe des Verfahrens durch die 2. Ableitung möglich. Hierzu sind drei Schritte nötig, welche sich aus dem Suchen eines möglichen Extrempunktes, dem Bilden der 2. Ableitung und dem Beweis der Existenz der Extremstelle zusammensetzt. Zunächst muss die Nullstelle der 1. Ableitung gesucht werden. Anschließend wird die 2. Ableitung gebildet und zu guter Letzt der x-Wert der möglichen Extremstelle in die 2. Ableitung eingesetzt. Hierbei wird darauf geachtet, ob die 2. Ableitung größer oder kleiner 0 ist. Falls sie größer 0 ist, tritt an dieser Stelle ein Minimum auf, falls sie kleiner 0 ist, tritt an dieser Stelle ein Maximum auf.
Da bei unserer gegebenen Funktion keine Extremstellen auftreten, werde ich an einem selbstgewählten Beispiel erklären, wie genau dieses Verfahren funktioniert.
Beispielaufgabe:
Bestimmung der Nullstelle der 1. Ableitung:
Beweis für Extrempunkt:
Daran dass die 2. Ableitung an der der Stelle des möglichen Extremwertes größer 0 ist, erkennt man eindeutig, dass es sich hierbei um ein Minimum der Funktion handelt. Ob dies ein lokales Minimum ist oder ein Minimum für die ganze Funktion ist, kann allerdings nur durch die Überprüfung der Grenzwerte festgestellt werden.
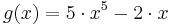
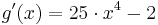
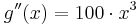
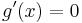
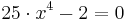
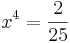
![x = \sqrt[4]{\frac {2}{25}}](/images/math/2/d/f/2df8033ed462bb75fb46d671d2698434.png)
![g''(\sqrt[4]{\frac {2}{25}}) = 100\cdot (\sqrt[4]{\frac {2}{25}})^{3} > 0](/images/math/8/a/7/8a748d3391bd1ebec89e17145ecee315.png)

