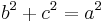Abzählmethode
Der Satz des Pythagoras
|
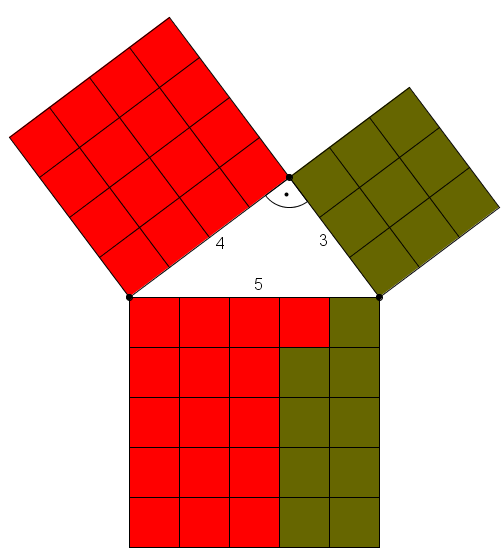
In jedem beliebigen rechtwinkligen Dreieck gilt der Satz des Pythagoras: Im speziellen rechtwinkligen Dreiecken mit den Katheten a und b und der Hypotenuse c gilt ebenfalls der Satz des Pythagoras.  Das ist die Form die häufig in der Literatur zu finden ist. Achte jedoch immer darauf, dass der Satz des Pythagoras nicht unbedingt so aussehen muss! Für ein rechtwinkliges Dreieck mit der Hypotenuse a und den Katheten b und c heißt der Satz des Pythagoras nämlich beispielsweise |
Arbeitsauftrag:
- Zeichne das rechtwinklige Dreieck
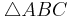 ab
ab
- Notiere dir den Satz des Pythagoras:
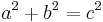
Die Abzählmethode
Es gibt neben dem Zerlegungsbeweis noch einen anderen Beweis zum Satz des Pythagoras.
Dieser funktioniert jedoch nur in rechtwinkligen Dreiecken mit ganzzahligen Seitenlängen (z.B. Hypotenuse=5cm, Kathete1=4cm und Kathete2=3cm)!
Ganze Zahlen a, b und c, die den Satz des Pythagoras, also die Gleichung 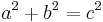 erfüllen, nennt man ein pythagoräisches Zahlentipel
erfüllen, nennt man ein pythagoräisches Zahlentipel
Man braucht also ein pythagoräisches Zahlentripel für die Abzählmethode, da man zum einen ein Dreieck mit ganzzahligen Seitenlängen braucht und auch ein Dreieck bei dem der Satz des Pythagoras gilt (da dieser ja bewiesen werden soll).
Einige pythagoräische Zahlentripel sind:
| Kathetea | 3 | 6 | 5 | 7 |
| Katheteb | 4 | 8 | 12 | 24 |
| Hypotenuse | 5 | 10 | 13 | 25 |
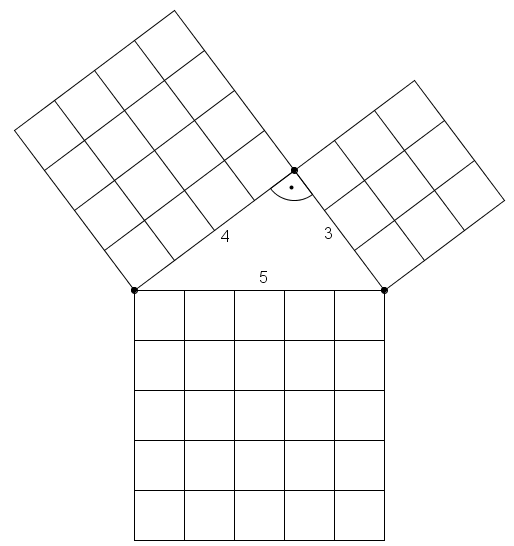
In der folgenden Zeichnung siehst du ein rechtwinkliges Dreieck mit einem pythagoräischen Zahlentripel als Seitenlängen. Die Quadrate über den Katheten und der Hypotenuse sind in gleichgroße Quadrate mit der Seitenlänge 1 aufgeteilt:
Arbeitsauftrag:
- Zähle die einzelnen kleinen Quadrate ab, die in den Quadraten über den Katheten eingezeichnet sind
- Versuche mit den kleinen Quadraten das Quadrat über der Hypotenuse zu füllen
- Was fällt dir auf?
- Man kann die kleinen Quadrate von den Quadraten über den Katheten im Quadrat über der Hypotenuse verteilen
- Man sieht also, dass sich die Quadrate über den Katheten auf das Quadrat über der Hypotenuse verteilen lassen
- d.h.
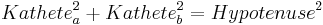
- Du hast damit den Satz des Pythagoras bewiesen!
Wenn du fertig bist geht es hier mit dem Brückenproblem weiter.
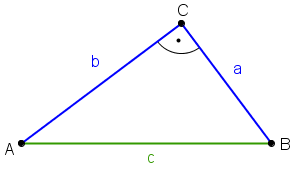
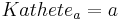 ,
, 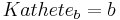 und
und 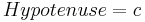 sieht der Satz so aus:
sieht der Satz so aus: