Satz des Pythagoras - Seite 3

Das Problem mit dem Stahlseil

In der nachfolgenden Skizze siehst du das Anfangsproblem mit dem Stahlseil an der Schrägseilbrücke noch einmal schematisch dargestellt.

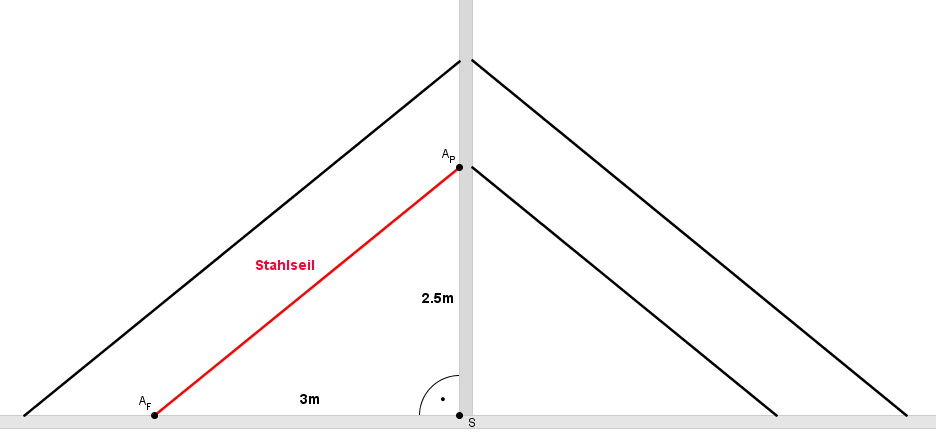
Man sieht den Aufhängungspunkt an der Fahrbahn (A_F), den Aufhängungspunkt am Pfeiler (A_P) und den Punkt in dem Fahrbahn und Pfeiler aufeinander treffen (S).
Aus den Konstruktionspapieren weiß man, dass der Pfeiler senkrecht auf die Fahrbahn steht, dass das Stahlseil 3m vom Pfeiler entfernt in der Fahrbahn verankert ist und dass das Seil 2,5m über dem Boden am Pfeiler befestigt wurde.

Wie könnte man nun die Länge des Stahlseiles mit Hilfe des bisher Gelernten berechnen?

[Lösung anzeigen][Lösung ausblenden]

• Das Dreieck 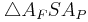$\triangle A_F S A_P$ ist ein rechtwinkliges Dreieck. ${[A_F S]\,}$ und ${[A_P S]\,}$ sind seine Katheten, ${[A_F A_P]\,}$ ist seine Hypotenuse
  
• Man kann also die Länge des Stahlseiles mit Hilfe des Satzes des Pythagoras berechnen

Arbeitsauftrag:

• Skizziere das Schema in dein Heft
• Notiere dir die Lösungsidee
• Berechne jetzt die Länge des Stahlseiles in deinem Heft!

[Lösung anzeigen][Lösung ausblenden]

• Man setzt zunächst den Satz des Pythagoras an:
• $(\overline{A_F A_P})^2=(\overline{A_F S})^2+(\overline{A_P S})^2$
• $(\overline{A_F A_P})^2=(3m)^2+(2,5m)^2$
• $\overline{A_F A_P}=\sqrt{(3m)^2+(2,5m)^2}\approx3,91m$
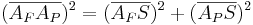
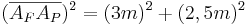
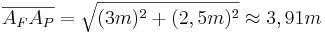
• Das Stahlseil müsste also etwa 3,91m lang sein
• Bravo! Gut gemacht! Jetzt wissen die Bauleiter wie lang ein Stahlseil sein muss, ohne dass jemand das Stahlseil ablaufen musste!

Neben dieser Anwendung gibt es jedoch auch noch andere. Hier erfährst du mehr über sie.