2003 VI
|
|
|
In einem kartesischen Koordinatensystem sind die Punkte , A(5|0|1), B(0|4|2) und C(0|0|t) mit 0 < t < 6 gegeben. |
a) Berechnen Sie für die Gerade AB den Schnittpunkt mit der x1 x2-Ebene sowie ihren Abstand d zur x3-Achse. (Teilergebnis: d 7 BE
3 BE
5 BE
|
Ferner ist der Punkt S(0|0|6) gegeben. A´, B´, C´ sind die Spurpunkte der Geraden SA, SB, SC in der Koordinatenebene x3 = 0. a) Bestimmen Sie die Koordinaten der Punkte A´, B´, C´. [Teilergebnis: A´(6|0|0), B´(0|6|0)]
4 BE
b) Legen Sie ein Koordinatensystem an (ganze Seite; Querformat; Koordinatenursprung in der Blattmitte). Tragen Sie darin die Pyramide A´B´C´S und das Dreieck ABC für t = 3 ein.
3 BE
4 BE
6 BE
|
Der Schnittpunkt von AB mit A´B´ heißt P, der von AC mit A´C´ bzw. BC mit B´C´ heißt Qt bzw. Rt
( a) Bringen Sie für t = 3 die genannten Geraden in Ihrer Zeichnung zum Schnitt.
2 BE
b) In Ihrer Zeichnung sollten P, Q3, R3 auf einer Geraden liegen.
6 BE
|
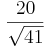 )
)
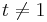 und
und 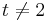 ).
).

