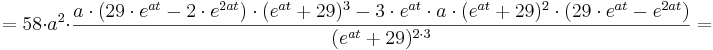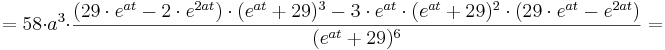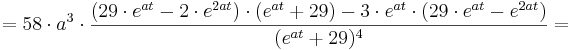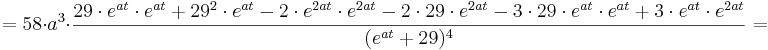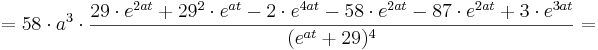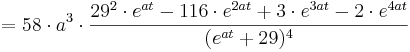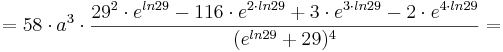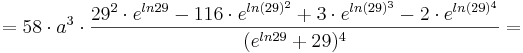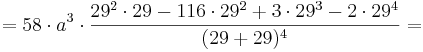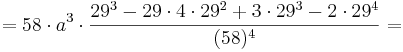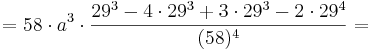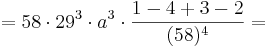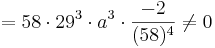3. Ableitung: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
Zeile 6: Zeile 6:
 
'''1. Teil: Bildung der 3. Ableitung:'''
 
'''1. Teil: Bildung der 3. Ableitung:'''
  
−
Bei der Bildung der 3. Ableitung muss wieder die [http://www.frustfrei-lernen.de/mathematik/ableitung-produktregel-quotientenregel-ableitungsregel.html Quotientenregel] und die [http://www.frustfrei-lernen.de/mathematik/ableitung-kettenregel.html Kettenregel] angewendet werden
+
Bei der Bildung der 3. Ableitung muss wieder die [http://www.frustfrei-lernen.de/mathematik/ableitung-produktregel-quotientenregel-ableitungsregel.html Quotientenregel] und die [http://www.frustfrei-lernen.de/mathematik/ableitung-kettenregel.html Kettenregel] angewendet werden.
 +
 
  
 
<math>f'''_{a} (t) = 58\cdot a^{2}\cdot \frac {(29\cdot e^{at}\cdot a - e^{2at}\cdot 2a)\cdot (e^{at} + 29)^{3} - 3\cdot (e^{at} + 29)^{2} \cdot e^{at}\cdot a\cdot (29\cdot e^{at} - e^{2at})} {((e^{at} + 29)^{3})^{2}} =</math>
 
<math>f'''_{a} (t) = 58\cdot a^{2}\cdot \frac {(29\cdot e^{at}\cdot a - e^{2at}\cdot 2a)\cdot (e^{at} + 29)^{3} - 3\cdot (e^{at} + 29)^{2} \cdot e^{at}\cdot a\cdot (29\cdot e^{at} - e^{2at})} {((e^{at} + 29)^{3})^{2}} =</math>
Zeile 33: Zeile 34:
  
 
<br />
 
<br />
−
Klicke [[Facharbeit Mathematik Straßheimer/Die Aufgabe/Lösung b)/Weitere Verfahren|hier]] um wieder zur Übersicht der beiden zusätzlichen Verfahren zu kommen, oder [[Facharbeit Mathematik Straßheimer/Die Aufgabe/Lösung b)|hier]] um wieder zur Lösung der Teilaufgabe b) zu gelangen.
+
[[Facharbeit Mathematik Straßheimer/Die Aufgabe/Lösung b)/Weitere Verfahren|Klicke hier]] um wieder zur Übersicht der beiden zusätzlichen Verfahren zu kommen, oder [[Facharbeit Mathematik Straßheimer/Die Aufgabe/Lösung b)|hier klicken]] um wieder zur Lösung der Teilaufgabe b) zu gelangen.

Version vom 28. Januar 2010, 23:26 Uhr

3. Möglichkeit: 3. Ableitung

Mit Hilfe der 3. Ableitung kann man ebenfalls herausfinden, ob an dem möglichen Wendepunkt auch wirklich einer vorhanden ist. Diese Variante benötigt ebenfalls zwei Teilschritte, welche zunächst die Bildung der 3. Ableitung ist. Im zweiten Teil muss man nun den t-Wert der möglichen Wendestelle einsetzen und sehen, ob die 3. Ableitung an dieser Stelle ungleich 0 ist. Falls dies der Fall ist, ist dies der eindeutige Beweis für die Existenz eines Wendepunkts.


1. Teil: Bildung der 3. Ableitung:

Bei der Bildung der 3. Ableitung muss wieder die Quotientenregel und die Kettenregel angewendet werden.


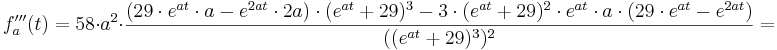
f'''_{a} (t) = 58\cdot a^{2}\cdot \frac {(29\cdot e^{at}\cdot a - e^{2at}\cdot 2a)\cdot (e^{at} + 29)^{3} - 3\cdot (e^{at} + 29)^{2} \cdot e^{at}\cdot a\cdot (29\cdot e^{at} - e^{2at})} {((e^{at} + 29)^{3})^{2}} =

= 58\cdot a^{2}\cdot \frac {a\cdot(29\cdot e^{at} - 2\cdot e^{2at} )\cdot (e^{at} + 29)^{3} - 3\cdot e^{at}\cdot a\cdot (e^{at} + 29)^{2} \cdot (29\cdot e^{at} - e^{2at})} {(e^{at} + 29)^{2\cdot 3}} =
= 58\cdot a^{3}\cdot \frac {(29\cdot e^{at} - 2\cdot e^{2at} )\cdot (e^{at} + 29)^{3} - 3\cdot e^{at}\cdot (e^{at} + 29)^{2} \cdot (29\cdot e^{at} - e^{2at})} {(e^{at} + 29)^{6}} =
= 58\cdot a^{3}\cdot \frac {(29\cdot e^{at} - 2\cdot e^{2at} )\cdot (e^{at} + 29) - 3\cdot e^{at}\cdot (29\cdot e^{at} - e^{2at})} {(e^{at} + 29)^{4}} =
= 58\cdot a^{3}\cdot \frac {29\cdot e^{at}\cdot e^{at} + 29^{2} \cdot e^{at} - 2\cdot e^{2at}\cdot e^{2at} - 2\cdot 29\cdot e^{2at} - 3\cdot 29\cdot e^{at}\cdot e^{at} + 3\cdot e^{at}\cdot e^{2at}} {(e^{at} + 29)^{4}} =
= 58\cdot a^{3}\cdot \frac {29\cdot e^{2at} + 29^{2} \cdot e^{at} - 2\cdot e^{4at} - 58\cdot e^{2at} - 87\cdot e^{2at} + 3\cdot e^{3at}} {(e^{at} + 29)^{4}} =
= 58\cdot a^{3}\cdot \frac {29^{2} \cdot e^{at} - 116\cdot e^{2at} + 3\cdot e^{3at} - 2\cdot e^{4at}} {(e^{at} + 29)^{4}}


2. Teil: Möglichen Wendepunkt in die 3. Ableitung einsetzen:

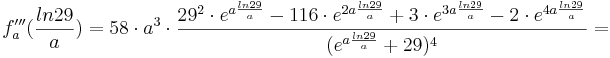
f'''_{a} (\frac {ln29} {a}) = 58\cdot a^{3}\cdot \frac {29^{2} \cdot e^{a \frac {ln29} {a}} - 116\cdot e^{2a \frac {ln29} {a}} + 3\cdot e^{3a \frac {ln29} {a}} - 2\cdot e^{4a \frac {ln29} {a}}} {(e^{a\frac {ln29} {a}} + 29)^{4}}=

= 58\cdot a^{3}\cdot \frac {29^{2} \cdot e^{ln29} - 116\cdot e^{2\cdot ln29} + 3\cdot e^{3\cdot ln29} - 2\cdot e^{4\cdot ln29}} {(e^{ln29} + 29)^{4}}=
= 58\cdot a^{3}\cdot \frac {29^{2} \cdot e^{ln29} - 116\cdot e^{ln(29)^{2}} + 3\cdot e^{ln(29)^{3}} - 2\cdot e^{ln(29)^{4}}} {(e^{ln29} + 29)^{4}}=
= 58\cdot a^{3}\cdot \frac {29^{2} \cdot 29 - 116\cdot 29^{2} + 3\cdot 29^{3} - 2\cdot 29^{4}} {(29 + 29)^{4}}=
= 58\cdot a^{3}\cdot \frac {29^{3} - 29\cdot 4\cdot 29^{2} + 3\cdot 29^{3} - 2\cdot 29^{4}} {(58)^{4}}=
= 58\cdot a^{3}\cdot \frac {29^{3} - 4\cdot 29^{3} + 3\cdot 29^{3} - 2\cdot 29^{4}} {(58)^{4}}=
= 58\cdot 29^{3} \cdot a^{3}\cdot \frac {1 - 4 + 3 - 2} {(58)^{4}}=
= 58\cdot 29^{3} \cdot a^{3}\cdot \frac {- 2} {(58)^{4}} \neq 0


Daraus folgt, dass an der Stelle 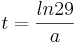t = \frac {ln29} {a} eindeutig ein Wendepunkt nachgewiesen wurde, da die 3. Ableitung an dieser Stelle ungleich 0 ist.



Klicke hier um wieder zur Übersicht der beiden zusätzlichen Verfahren zu kommen, oder hier klicken um wieder zur Lösung der Teilaufgabe b) zu gelangen.

Von „http://rmg.zum.de/index.php?title=Facharbeit_Mathematik_Straßheimer/Die_Aufgabe/Lösung_b)/Weitere_Verfahren/3._Ableitung&oldid=28566“