Teilaufgabe a: Unterschied zwischen den Versionen
Aus RMG-Wiki
| Zeile 19: | Zeile 19: | ||
Alle Extrempunkte für <math>a\in R</math> befinde sich auf einer Parallelen zur x-Achse mit <math>y=e\;</math>.<br /> Das heißt, dass alle Extrempunkte auf dem Graphen der Funktion <math>H ( x ) = e\;</math> liegen. | Alle Extrempunkte für <math>a\in R</math> befinde sich auf einer Parallelen zur x-Achse mit <math>y=e\;</math>.<br /> Das heißt, dass alle Extrempunkte auf dem Graphen der Funktion <math>H ( x ) = e\;</math> liegen. | ||
}}<br /> | }}<br /> | ||
| − | |||
| − | |||
:3.Skizzieren Sie den Graphen der Funktion '''f<sub>2</sub>''' für '''1,6 <u><</u> x <u><</u>7!''' | :3.Skizzieren Sie den Graphen der Funktion '''f<sub>2</sub>''' für '''1,6 <u><</u> x <u><</u>7!''' | ||
| − | + | {{Lösung versteckt| | |
| + | Graph der Funktion f<sub>2</sub> für 1,6 <u><</u> x <u><</u> 7 | ||
| + | }}<br /> | ||
[[Lösung zur Teilaufgabe a)]] | [[Lösung zur Teilaufgabe a)]] | ||
Version vom 21. Januar 2010, 23:02 Uhr
Für jede reelle Zahl a sei eine Funktion fa durch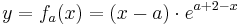 
mit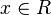 
gegeben.
- 1.Untersuchen Sie den Graphen von fa auf:
- Schnittpunkte mit den Koordinatenachsen,
Lösung: Schnittpunkte mit den Koordinatenachsen - lokale Extrempunkte und
Lösung: lokale Extrempunkte - Wendepunkte!
Lösung: Wendepunkte
- Schnittpunkte mit den Koordinatenachsen,
- Bestimmen Sie gegebenenfalls deren Koordinaten!
- 2.Alle Extrempunkte liegen auf dem Graphen einer Funktion h. Geben Sie eine Funktionsgleichung von h an!
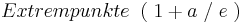
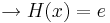
Alle Extrempunkte für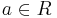 
befinde sich auf einer Parallelen zur x-Achse mit 
.
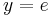Das heißt, dass alle Extrempunkte auf dem Graphen der Funktion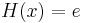 
liegen.
- 3.Skizzieren Sie den Graphen der Funktion f2 für 1,6 < x <7!
Graph der Funktion f2 für 1,6 < x < 7
