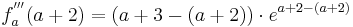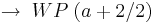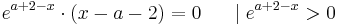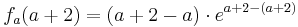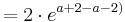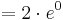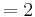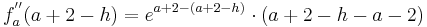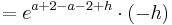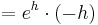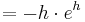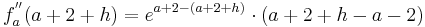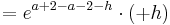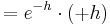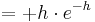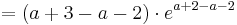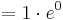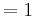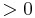Lösung: Wendepunkte: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
(→‎Wendepunkte)
(→‎Wendepunkte)
Zeile 2: Zeile 2:
  
 
== Wendepunkte ==
 
== Wendepunkte ==
 +
 +
Zweite Ableitung: siehe Überprüfung des Extrempunkts; 2. Möglichkeit
  
 
<math>f_a^{''} (x) = e^{a+2-x}\cdot ( x - a - 2 )</math>
 
<math>f_a^{''} (x) = e^{a+2-x}\cdot ( x - a - 2 )</math>
  
 
Um mögl. Wendepunkte zu bestimmen benötigt man die zweite Ableitung.
 
Um mögl. Wendepunkte zu bestimmen benötigt man die zweite Ableitung.
−
 
−
Zweite Ableitung: siehe Überprüfung des Extrempunkts; 2. Möglichkeit
 
−
 
  
 
Mögl. Wendepunkte tretten für <math>f_a^{''} (x) = 0\;</math> auf.
 
Mögl. Wendepunkte tretten für <math>f_a^{''} (x) = 0\;</math> auf.
Zeile 49: Zeile 48:
  
 
   
 
   
−
<math>\rightarrow VZW bei x = a + 2</math><br />
+
<math>\rightarrow \; VZW \; bei\; x = a + 2</math><br />
−
<math>\rightarrow  Wendepunkt bei ( a + 2 / 2 )</math>
+
<math>\rightarrow  \;Wendepunkt bei \;( a + 2 / 2 )</math>
  
  
Zeile 104: Zeile 103:
  
  
−
2. Möglichkeit
+
 
 +
==== 2. Möglichkeit ====
 +
 
 
Verwendung der dritten Ableitung
 
Verwendung der dritten Ableitung
  
−
f<sub>a</sub> (x) = ( x - a ) e<sup>a + 2 - x</sup>
+
<math>f_a (x) = e^{a+2-x}\cdot ( x - a)</math>
  
−
f<sub>a</sub><sup>'</sup> (x) = e<sup>a + 2 - x </sup> ( 1 + a - x )
+
<math>f_a^{'} (x) = e^{a+2-x}\cdot ( 1+a-x )</math>
 +
 
 +
<math>f_a^{''} (x) = e^{a+2-x}\cdot ( x - a - 2 )</math>
  
−
f<sub>a</sub><sup>''</sup> (x) = e<sup>a + 2 - x </sup> ( x - a - 2 )
 
  
 
Um die dritte Ableitung zu bekommen muss man hier die Produktregel verwenden.
 
Um die dritte Ableitung zu bekommen muss man hier die Produktregel verwenden.
 
[[http://de.wikipedia.org/wiki/Produktregel Hilfe zur Produktregel]]
 
[[http://de.wikipedia.org/wiki/Produktregel Hilfe zur Produktregel]]
  
−
f<sub>a</sub><sup>'''</sup> (x) = e<sup>a + 2 - x </sup> ( x - a - 2 ) (-1) + 1 e<sup>a + 2 - x </sup>
+
f_a^{'''} (x) = e^{a+2-x}\cdot ( x - a - 2 )\cdot (-1) + 1\cdot e^{a+2-x}
−
                                 = e<sup>a + 2 - x </sup> ( a + 2 - x + 1 )
+
                                 = e^{a+2-x}\cdot ( a + 2 - x + 1 )
−
                                 = ( a + 3 - x ) e<sup>a + 2 - x </sup>
+
                                 = ( a + 3 - x )\cdot e^{a+2-x}
  
 
Wenn die dritte Ableitung am möglichen Wendepunkt ungleich Null ist, liegt ein Wendepunkt vor.
 
Wenn die dritte Ableitung am möglichen Wendepunkt ungleich Null ist, liegt ein Wendepunkt vor.
  
−
f<sub>a</sub><sup>'''</sup> ( a + 2 ) = ( a + 3 - ( a + 2 )) e<sup>a + 2 - ( a + 2 ) </sup>
+
<math>f_a^{'''} ( a + 2 ) = ( a + 3 - ( a + 2 ))\cdot e^{a + 2 - ( a + 2 )}</math>
−
                                       = ( a + 3 - a - 2 ) e<sup>a + 2 - a - 2 ) </sup>
+
                                       <math>= ( a + 3 - a - 2 ) \cdot e^{a + 2 - a - 2 }</math>
−
                                       = 1 e^0
+
                                       <math>= 1\cdot e^{0}</math>
−
                                       = 1  
+
                                       <math>= 1\;</math>
−
                                       > 0
+
                                       <math>> 0\;</math>
  
−
--> WP ( a + 2 / 2 )
+
<math>\rightarrow \; WP \;( a + 2 / 2 )</math>

Version vom 19. Januar 2010, 23:25 Uhr

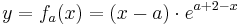y = f_a (x) = ( x - a )\cdot e^{a+2-x} mit x\in R ; a\in R

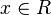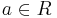
Inhaltsverzeichnis

Wendepunkte

Zweite Ableitung: siehe Überprüfung des Extrempunkts; 2. Möglichkeit

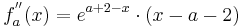
f_a^{''} (x) = e^{a+2-x}\cdot ( x - a - 2 )

Um mögl. Wendepunkte zu bestimmen benötigt man die zweite Ableitung.

Mögl. Wendepunkte tretten für 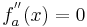f_a^{''} (x) = 0\; auf. 

f_a^{''} (x) = 0\;

e^{a+2-x}\cdot ( x - a - 2 ) = 0    \;\;\;\;\;\; | \; e^{a+2-x} > 0

    \rightarrow \; ( x - a - 2 ) = 0 \;\;\;\;\;\; | \;  + 2 ; + a

               x = a + 2\;

Möglicher Wendepunkt bei 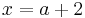x = a + 2 \; 


f_a ( a + 2 ) = ( a + 2 - a )\cdot e^{a+2-(a + 2 )}

                       = 2\cdot e^{a+2-a - 2 )}

                       = 2\cdot e^0

                       = 2\;

\rightarrow mög. WP \; ( a + 2 / 2 )


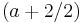
Überprüfung des Wendepunkts

1. Möglichkeit

H-Methode , VZW des Krümmungsverhaltens 

f_a^{''} ( a + 2  - h ) = e^{a + 2 - (a + 2 - h )}\cdot ( a + 2 - h - a - 2 )

                                          = e^{a + 2 - a- 2 + h }\cdot (- h)

                                          = e^{h }\cdot ( -h )

                                          = -h\cdot e^{h }

                                          lim h --> 0 ............

f_a^{''} ( a + 2 +  h ) = e^{a + 2 - (a + 2 + h )}\cdot ( a + 2 + h - a - 2 )

                                          = e^{a + 2 - a- 2 - h }\cdot (+ h)

                                          = e^{-h }\cdot ( +h )

                                          = +h\cdot e^{-h }

                                          lim h --> 0 ............


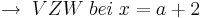
\rightarrow \; VZW \; bei\; x = a + 2
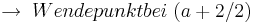
\rightarrow \;Wendepunkt bei \;( a + 2 / 2 )


zur Verdeutlichung

Krümmungsverhalten
x<2+a x=2+a x>2+a
ea + 2 - x + +
( x - a - 2 ) - +
fa ( x ) - +

--> WP ( a + 2 / 2 )


2. Möglichkeit

Verwendung der dritten Ableitung

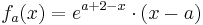
f_a (x) = e^{a+2-x}\cdot ( x - a)

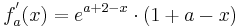
f_a^{'} (x) = e^{a+2-x}\cdot ( 1+a-x )

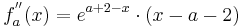
f_a^{''} (x) = e^{a+2-x}\cdot ( x - a - 2 )


Um die dritte Ableitung zu bekommen muss man hier die Produktregel verwenden. [Hilfe zur Produktregel]

f_a^{} (x) = e^{a+2-x}\cdot ( x - a - 2 )\cdot (-1) + 1\cdot e^{a+2-x} 

                               = e^{a+2-x}\cdot ( a + 2 - x + 1 )
                               = ( a + 3 - x )\cdot e^{a+2-x}

Wenn die dritte Ableitung am möglichen Wendepunkt ungleich Null ist, liegt ein Wendepunkt vor.

f_a^{'''} ( a + 2 ) = ( a + 3 - ( a + 2 ))\cdot e^{a + 2 - ( a + 2 )} 

                                     = ( a + 3 - a - 2 ) \cdot e^{a + 2 -  a - 2 }
                                     = 1\cdot e^{0}
                                     = 1\; 
                                     > 0\;

\rightarrow \; WP \;( a + 2 / 2 )

Von „http://rmg.zum.de/index.php?title=Facharbeit_Andre_Etzel/Teilaufgabe_a/Lösung:_Wendepunkte&oldid=27322“