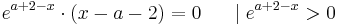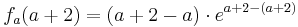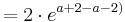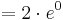Lösung: Wendepunkte: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: === Wendepunkte === Zweite Ableitung siehe: Überprüfung des Extrempunkts; 2. Möglichkeit f<sub>a</sub><sup>''</sup> (x) = e<sup>a + 2 - x </sup> ( x - a - 2 ) Um...)
 
Zeile 1: Zeile 1:
−
=== Wendepunkte ===
+
<math>y  = f_a (x) = ( x - a )\cdot e^{a+2-x}</math> mit <math>x\in R</math> ; <math>a\in R</math>
  
−
Zweite Ableitung siehe: Überprüfung des Extrempunkts; 2. Möglichkeit
+
== Wendepunkte ==
 +
Um mögl. Wendepunkte zu bestimmen benötigt man die zweite Ableitung.
  
−
f<sub>a</sub><sup>''</sup> (x) = e<sup>a + 2 - x </sup> ( x - a - 2 )
+
Zweite Ableitung: siehe Überprüfung des Extrempunkts; 2. Möglichkeit
  
−
Um mögl. Wendepunkte zu bestimmen benötigt man die zweite Ableitung
+
<math>f_a^{''} (x) = e^{a+2-x}\cdot ( x - a - 2 )</math>
  
−
Mögl. Wendepunkte tretten für f<sub>a</sub><sup>''</sup> (x) = 0 auf.
 
  
−
f<sub>a</sub><sup>''</sup> (x) = 0
+
Mögl. Wendepunkte tretten für <math>f_a^{''} (x) = 0\;</math> auf.
  
−
e<sup>a + 2 - x </sup> ( x - a - 2 ) = 0       / e<sup>a + 2 - x </sup> > 0
+
<math>f_a^{''} (x) = 0\;</math><br />
 +
<math>e^{a+2-x}\cdot ( x - a - 2 ) = 0    \;\;\;\;\;\; | \; e^{a+2-x} > 0</math><br />
 +
    <math> \rightarrow \; ( x - a - 2 ) = 0 \;\;\;\;\;\; | \;  + 2 ; + a</math><br />
 +
                <math>x = a + 2\;</math><br />
  
−
  -->   ( x - a - 2 ) = 0                      / + 2 ; + a
+
Möglicher Wendepunkt bei <math>x = a + 2 \; </math>
  
−
          x = a + 2
 
  
−
Möglicher Wendepunkt bei x = a + 2
+
<math>f_a ( a + 2 ) = ( a + 2 - a )\cdot e^{a+2-(a + 2 )}</math><br />
 +
                      <math> = 2\cdot e^{a+2-a - 2 )}</math><br />
 +
                      <math> = 2\cdot e^0</math><br />
 +
                      <math> = 2\;</math><br />
  
−
f<sub>a</sub> ( a + 2 ) = ( a + 2 - a ) e<sup>a + 2 - (a + 2 )</sup>
+
<math> \rightarrow </math>   mög. WP <math>\; ( a + 2 / 2 )</math>
−
                        = 2 e<sup>a + 2 - a - 2 )</sup>
+
−
                        = 2 e^0
+
−
                        = 2
+
  
−
    mög. WP ( a + 2 / 2 )
 
  
  
 +
=== Überprüfung des Wendepunkts ===
  
−
==== Überprüfung des Wendepunkts ====
 
  
−
1. Möglichkeit
+
==== 1. Möglichkeit ====
 
H-Methode , VZW des Krümmungsverhaltens
 
H-Methode , VZW des Krümmungsverhaltens
  

Version vom 16. Januar 2010, 00:47 Uhr

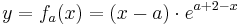y = f_a (x) = ( x - a )\cdot e^{a+2-x} mit x\in R ; a\in R

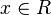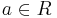
Wendepunkte

Um mögl. Wendepunkte zu bestimmen benötigt man die zweite Ableitung.

Zweite Ableitung: siehe Überprüfung des Extrempunkts; 2. Möglichkeit

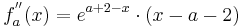
f_a^{''} (x) = e^{a+2-x}\cdot ( x - a - 2 )


Mögl. Wendepunkte tretten für 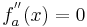f_a^{''} (x) = 0\; auf. 

f_a^{''} (x) = 0\;

e^{a+2-x}\cdot ( x - a - 2 ) = 0    \;\;\;\;\;\; | \; e^{a+2-x} > 0

    \rightarrow \; ( x - a - 2 ) = 0 \;\;\;\;\;\; | \;  + 2 ; + a

               x = a + 2\;

Möglicher Wendepunkt bei 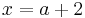x = a + 2 \; 


f_a ( a + 2 ) = ( a + 2 - a )\cdot e^{a+2-(a + 2 )}

                       = 2\cdot e^{a+2-a - 2 )}

                       = 2\cdot e^0

                       = 2\;

\rightarrow mög. WP \; ( a + 2 / 2 )


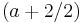
Überprüfung des Wendepunkts

1. Möglichkeit

H-Methode , VZW des Krümmungsverhaltens

fa ( a + 2 + - h ) = ea + 2 - (a + 2 - h ) ( a + 2 - h - a - 2 ) 

                                          = ea + 2 - a - 2 + h )  ( -h )
                                          = e^h ( -h )
                                          = -h e^h
                                          lim h --> 0 ............

fa ( a + 2 + + h ) = ea + 2 - (a + 2 + h ) ( a + 2 + h - a - 2 ) 

                                          = ea + 2 - a - 2 - h )  ( h )
                                          = e^h ( h )
                                          = h e^h

                                          lim h --> 0 ............


--> VZW bei x = a + 2
--> Wendepunkt bei ( a + 2 / 2 )

zur Verdeutlichung

Krümmungsverhalten
x<2+a x=2+a x>2+a
ea + 2 - x + +
( x - a - 2 ) - +
fa ( x ) - +

--> WP ( a + 2 / 2 )


2. Möglichkeit Verwendung der dritten Ableitung

fa (x) = ( x - a ) ea + 2 - x

fa' (x) = ea + 2 - x ( 1 + a - x )

fa (x) = ea + 2 - x ( x - a - 2 )

Um die dritte Ableitung zu bekommen muss man hier die Produktregel verwenden. [Hilfe zur Produktregel]

fa (x) = ea + 2 - x ( x - a - 2 ) (-1) + 1 ea + 2 - x 

                               = ea + 2 - x  ( a + 2 - x + 1 )
                               = ( a + 3 - x ) ea + 2 - x

Wenn die dritte Ableitung am möglichen Wendepunkt ungleich Null ist, liegt ein Wendepunkt vor.

fa ( a + 2 ) = ( a + 3 - ( a + 2 )) ea + 2 - ( a + 2 ) 

                                     = ( a + 3 - a - 2 ) ea + 2 - a - 2 ) 
                                     = 1 e^0
                                     = 1 
                                     > 0

--> WP ( a + 2 / 2 )

Von „http://rmg.zum.de/index.php?title=Facharbeit_Andre_Etzel/Teilaufgabe_a/Lösung:_Wendepunkte&oldid=26909“