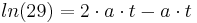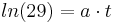Lösung b): Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
(→‎Suche nach dem Wendepunkt:)
Zeile 40: Zeile 40:
 
  <math>ln(29) = a\cdot t</math>
 
  <math>ln(29) = a\cdot t</math>
 
  <math>t = \frac {ln29} {a}</math>
 
  <math>t = \frac {ln29} {a}</math>
 +
 +
===<u>Beweis für Wendepunkt:</u>===
 +
 +
====1. Möglichkeit:====
 +
 +
====2. Möglichkeit:====
 +
 +
====3. Möglichkeit:====
 +
  
 
==Zeichnen sie die Graphen G<sub>0,75</sub> und G<sub>1</sub> in ein und dasselbe Koordinatensystem und schlussfolgern Sie, welchen Einfluss der Parameter a auf den Verlauf der Graphen G<sub>a</sub> hat==
 
==Zeichnen sie die Graphen G<sub>0,75</sub> und G<sub>1</sub> in ein und dasselbe Koordinatensystem und schlussfolgern Sie, welchen Einfluss der Parameter a auf den Verlauf der Graphen G<sub>a</sub> hat==

Version vom 10. Januar 2010, 12:37 Uhr

y = f_{a}(t) = \frac{2\cdot e^{at}}{e^{at}+29}, t\in R, a\in R, a>0

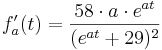
f'_{a} (t) = \frac{58\cdot a\cdot e^{at} }{(e^{at}+29) ^{2}}

Inhaltsverzeichnis

Untersuchen sie die Funktionen fa auf Nullstellen und lokale Extremstellen

Suche nach Nullstellen:

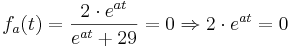
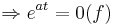
f_{a}(t) = \frac{2\cdot e^{at}}{e^{at}+29} = 0 \Rightarrow 2\cdot e^{at} = 0 \Rightarrow e^{at} = 0 (f)

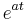\Rightarrow keine Nullstellen, da die e-Fkt. nie 0 wird und somit der Ausdruck e^{at} ebenfalls nie 0 werden kann

Suche nach Extremstellen:

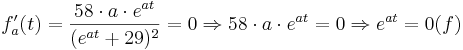
f'_{a} (t) = \frac{58\cdot a\cdot e^{at} }{(e^{at}+29) ^{2}} = 0 \Rightarrow 58\cdot a \cdot e^{at} = 0 \Rightarrow e^{at} = 0 (f)

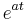\Rightarrow keine Extremstellen, da die e-Fkt. nie 0 wird und somit der Ausdruck e^{at} ebenfalls nie 0 werden kann


Jeder Graph Ga bestitzt genau einen Wendepunkt Wa. Zeigen sie, dass die Wendepunkte Wa auf einer parallelen zur t-Achse liegen

Die 2. Ableitung:

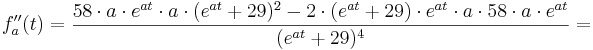
f''_{a}(t) = \frac{58\cdot a \cdot e^{at}\cdot a\cdot(e^{at}+29)^{2} - 2 \cdot(e^{at} + 29)\cdot e^{at}\cdot a \cdot 58 \cdot a \cdot e^{at} }{(e^{at} + 29) ^{4} } =
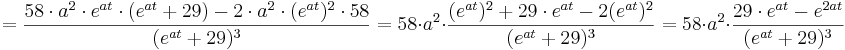
= \frac{58\cdot a^{2} \cdot e^{at}\cdot (e^{at} + 29) - 2\cdot a^{2} \cdot (e^{at})^{2}\cdot 58 }{(e^{at}+29)^{3}} = 58\cdot a^{2}\cdot \frac{(e^{at})^{2} + 29\cdot e^{at} - 2(e^{at})^2}{(e^{at} + 29)^{3}} = 58\cdot a^{2} \cdot \frac {29\cdot e^{at} - e^{2at}}{(e^{at}+29)^{3}}

Suche nach dem Wendepunkt:

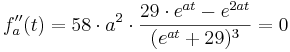
f''_{a}(t) = 58\cdot a^{2} \cdot \frac {29\cdot e^{at} - e^{2at}}{(e^{at}+29)^{3}} = 0 

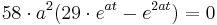
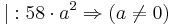
58\cdot a^{2} (29\cdot e^{at} - e^{2at}) = 0    | : 58\cdot a^{2} \Rightarrow (a \neq 0)
(29\cdot e^{at} - e^{2at}) = 0          | + e^{2at}
29 \cdot e^{at} = e^{2at}                | ln
ln(29\cdot e^{at}) = ln(e^{2at})
ln(29) + ln(e^{at}) = ln(e^{2at})            | - ln(e^{at})
ln(29) = ln(e^{2at}) - ln(e^{at})
ln(29) = 2\cdot a\cdot t \cdot ln(e) - a\cdot t\cdot ln(e)    (ln(e)=1)
ln(29) = 2\cdot a\cdot t - a\cdot t
ln(29) = a\cdot t
t = \frac {ln29} {a}

Beweis für Wendepunkt:

1. Möglichkeit:

2. Möglichkeit:

3. Möglichkeit:

Zeichnen sie die Graphen G0,75 und G1 in ein und dasselbe Koordinatensystem und schlussfolgern Sie, welchen Einfluss der Parameter a auf den Verlauf der Graphen Ga hat

Von „http://rmg.zum.de/index.php?title=Facharbeit_Mathematik_Straßheimer/Die_Aufgabe/Lösung_b)&oldid=26113“