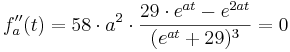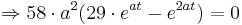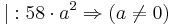Lösung b): Unterschied zwischen den Versionen
Aus RMG-Wiki
K (Die Seite wurde neu angelegt: <math>y = f_{a}(t) = \frac{2\cdot e^{at}}{e^{at}+29}</math>, <math>t\in R, a\in R, a>0</math> ==Untersuchen sie die Funktionen f<sub>a</sub> auf Nullstellen und ...) |
|||
| Zeile 1: | Zeile 1: | ||
| − | + | <math>y = f_{a}(t) = \frac{2\cdot e^{at}}{e^{at}+29}</math>, <math>t\in R, a\in R, a>0</math> | |
| + | |||
| + | <math>f'_{a} (t) = \frac{58\cdot a\cdot e^{at} }{(e^{at}+29) ^{2}} </math> | ||
==Untersuchen sie die Funktionen f<sub>a</sub> auf Nullstellen und lokale Extremstellen== | ==Untersuchen sie die Funktionen f<sub>a</sub> auf Nullstellen und lokale Extremstellen== | ||
| + | |||
| + | <math>f''_{a}(t) = \frac{58\cdot a \cdot e^{at}\cdot a\cdot(e^{at}+29)^{2} - 2 \cdot(e^{at} + 29)\cdot e^{at}\cdot a \cdot 58 \cdot a \cdot e^{at} }{(e^{at} + 29) ^{4} } =</math><br /> | ||
| + | <math>= \frac{58\cdot a^{2} \cdot e^{at}\cdot (e^{at} + 29) - 2\cdot a^{2} \cdot (e^{at})^{2}\cdot 58 }{(e^{at}+29)^{3}} = 58\cdot a^{2}\cdot \frac{(e^{at})^{2} + 29\cdot e^{at} - 2(e^{at})^2}{(e^{at} + 29)^{3}} = 58\cdot a^{2} \cdot \frac {29\cdot e^{at} - e^{2at}}{(e^{at}+29)^{3}}</math> | ||
| + | |||
| + | ===<u>Suche nach dem Wendepunkt:</u>=== | ||
| + | |||
| + | <math>f''_{a}(t) = 58\cdot a^{2} \cdot \frac {29\cdot e^{at} - e^{2at}}{(e^{at}+29)^{3}} = 0 </math> | ||
| + | <math>\Rightarrow 58\cdot a^{2} (29\cdot e^{at} - e^{2at}) = 0</math> <math>| : 58\cdot a^{2} \Rightarrow (a \neq 0) | ||
| + | </math> | ||
Version vom 6. Januar 2010, 14:22 Uhr
,
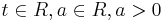
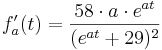
Untersuchen sie die Funktionen fa auf Nullstellen und lokale Extremstellen
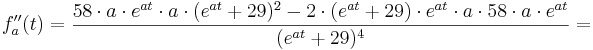
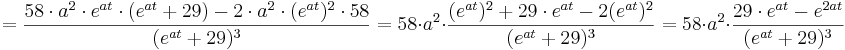
Suche nach dem Wendepunkt: