Lösung a) aa): Unterschied zwischen den Versionen
Aus RMG-Wiki
| Zeile 3: | Zeile 3: | ||
==Untersuchen sie das Verhalten der Funktionen f<sub>a</sub> für t -> <math>\pm \infty </math> und geben sie für die Asymptoten Gleichungen an.== | ==Untersuchen sie das Verhalten der Funktionen f<sub>a</sub> für t -> <math>\pm \infty </math> und geben sie für die Asymptoten Gleichungen an.== | ||
| − | Verhalten gegen <math>+\infty </math>: | + | ===<u>Verhalten gegen <math>+\infty </math></u>:=== |
| − | + | ||
<math>\lim_{t \to \infty } f(t) = \lim_{t \to \infty } \frac{2\cdot e^{at} }{e^{at}+29 } = 2 \cdot \lim_{t \to \infty }\frac{e^{at} }{e^{at}+29 } = 2\cdot 1 = 2</math> | <math>\lim_{t \to \infty } f(t) = \lim_{t \to \infty } \frac{2\cdot e^{at} }{e^{at}+29 } = 2 \cdot \lim_{t \to \infty }\frac{e^{at} }{e^{at}+29 } = 2\cdot 1 = 2</math> | ||
Da stets gilt a > 0, geht der Term <math>\lim_{t \to \infty } e^{at} </math> immer gegen <math>+\infty </math>; | Da stets gilt a > 0, geht der Term <math>\lim_{t \to \infty } e^{at} </math> immer gegen <math>+\infty </math>; | ||
| − | Daraus folgt nun, dass der Term <math>\lim_{t \to \infty } \frac{2\cdot e^{at} }{e^{at}+29 }</math> gegen 1 gehen muss, da 29 im Vergleich zu <math>+\infty </math> verschwinden klein ist | + | Daraus folgt nun, dass der Term <math>\lim_{t \to \infty } \frac{2\cdot e^{at} }{e^{at}+29 }</math> gegen 1 gehen muss, da 29 im Vergleich zu <math>+\infty </math> verschwinden klein ist. |
| + | |||
| + | ===<u>Verhalten gegen <math>-\infty </math></u>:=== | ||
| + | <math>\lim_{t \to - \infty } f(t) = 2\cdot \lim_{t \to -\infty } \frac{e^{at}}{e^{at}+29 } = 2\cdot \frac{0}{29} = 0</math> | ||
| + | |||
| + | Da stets gilt a > 0, geht der Term <math>\lim_{t \to - \infty } e^{at} </math> immer gegen <math>0</math>; Daraus folgt, dass der Zähler gegen 0 geht und der Nenner gegen 29. Wenn man nun 0 durch 29 teilt, erkennt man, dass der Grenzwert <math>\lim_{t \to -\infty } f(t) </math> gegen 0 geht. | ||
Version vom 3. Januar 2010, 15:37 Uhr
,
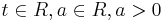
Untersuchen sie das Verhalten der Funktionen fa für t ->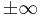 
und geben sie für die Asymptoten Gleichungen an.
Verhalten gegen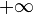 
:
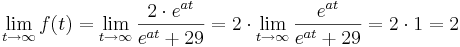
Da stets gilt a > 0, geht der Term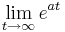 
immer gegen ;
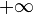Daraus folgt nun, dass der Term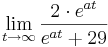 
gegen 1 gehen muss, da 29 im Vergleich zu 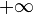verschwinden klein ist.
Verhalten gegen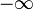 
:
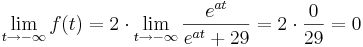
Da stets gilt a > 0, geht der Term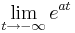 
immer gegen 
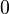; Daraus folgt, dass der Zähler gegen 0 geht und der Nenner gegen 29. Wenn man nun 0 durch 29 teilt, erkennt man, dass der Grenzwert 
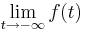gegen 0 geht.
