Die lineare Funktion: Unterschied zwischen den Versionen
(tiefgestellte Indizes) |
|||
| Zeile 33: | Zeile 33: | ||
den waagrechten Zuwachs, <math>\delta x</math>, und den Höhenzuwachs, <math>\delta y</math>, anzeigen.<br /> | den waagrechten Zuwachs, <math>\delta x</math>, und den Höhenzuwachs, <math>\delta y</math>, anzeigen.<br /> | ||
<math>\delta x</math> und <math>\delta y</math> ist jeweils die Differenz aus den beiden x- bzw. y-Werten der Punkte A und B.<br /> | <math>\delta x</math> und <math>\delta y</math> ist jeweils die Differenz aus den beiden x- bzw. y-Werten der Punkte A und B.<br /> | ||
| − | → <math>\delta x</math> = <math> | + | → <math>\delta x</math> = <math>x_B</math> - <math>x_A</math> = 4 - 2 = 2 <math>\delta y</math> = <math>yB</math> - <math>yA</math> = 2 - 1 = 1<br /> |
Der Quotient "'''Höhenzuwachs''' durch '''waagrechten Zuwachs'''" ergibt die Steigung m.<br /> | Der Quotient "'''Höhenzuwachs''' durch '''waagrechten Zuwachs'''" ergibt die Steigung m.<br /> | ||
m = <math>\frac{\partial x}{\partial y}</math> = <math>\frac{1}{2} </math> <br /> | m = <math>\frac{\partial x}{\partial y}</math> = <math>\frac{1}{2} </math> <br /> | ||
Version vom 9. Oktober 2009, 18:22 Uhr
Inhaltsverzeichnis |
Geradengleichung
Ufos versenken
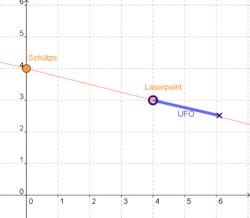
Zum Einstieg ein kleines Spiel!
Beim Ufos versenken geht es darum dem Schützen so genau wie möglich die Daten für die Schusslinie mitzuteilen, damit dieser dann erfolgreich die feindlichen Ufos abwehren kann.
Er muss zum einen wissen von welcher Position aus er schießen muss und zum andern welche Richtung er anpeilen muss.
Peile mit dem Laserpoint (rotes Kreuz) jeweils den Bug (blauer Kreis) des Ufos an und richte dann die Schusslinie so aus, dass sie auch das Heck (blaues Kreuz) genau durchläuft. Hierzu kannst du sowohl Schütze als auch Laserpoint mit der Maus verschieben.
Trage die Koordinaten anschließend auf deinem Arbeitsblatt ein und vergleiche zum Schluss deine Ergebnisse!
Hier ein Beispiel:
| Schütze | Laserpoint |
| 4 | -1 / 4 |
y-Abschnitt
Steigungsdreieck
Du hast dem Schützen nun zwei wichtige Informationen mitgeteilt, mit deren Hilfe sich die Schusslinie - eine Gerade - aufstellen lässt.
Zuerst einmal die Steigung: Sie wird in der Mathematik mit m bezeichnet!
Indem du vom Schützen ausgehend die Lage des Laserpoints ermittelt hast, hast du nicht anderes getan, als ein sogenanntes Steigunsdreieck zu beschreiben.
Im Beispiel gehen wir vom Punkt A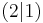 
aus um 2 Einheiten nach rechts,
um eine Einheit nach oben und kommen so bei Punkt B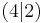 
wieder an. Daraus entsteht das rechtwinklige Steigungsdreieck, dessen Katheten einmal
den waagrechten Zuwachs,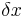 
, und den Höhenzuwachs, 
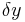, anzeigen.
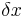und 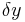ist jeweils die Differenz aus den beiden x- bzw. y-Werten der Punkte A und B.
→ = 
- 
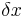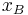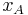= 4 - 2 = 2 = 
- 
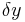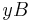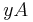= 2 - 1 = 1
Der Quotient "Höhenzuwachs durch waagrechten Zuwachs" ergibt die Steigung m.
m =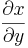 
= 
Dabei ist es völlig egal bei welchem Punkt man startet bzw. wie groß das Steigungsdreieck ist,
da das Verhältnis der beiden Katheten immer das gleiche bleibt.
Nehmen wir zum Beipiel das zweite Steigungsdreieck:
m = 
=
→ Die Steigung m dieser Geraden beträgt also an jeder Stelle 0,5!
Die Steigung kann natürlich auch negativ sein, dann ist der Graf der Geraden "fallend".
Versuche die Steigung unseres "Ufo-Beispiels" zu bestimmen.
Steigung m: m =
