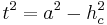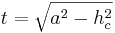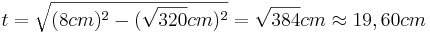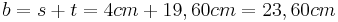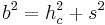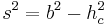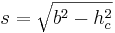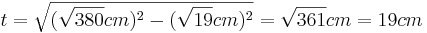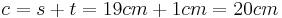Übungen zu Kehrsatz: Unterschied zwischen den Versionen
Aus RMG-Wiki
(Verlinkung eingefügt) |
(Arbeitsauftrag erweitert) |
||
| Zeile 1: | Zeile 1: | ||
| − | Hole dir das '''Übungsblatt zum Kehrsatz zum Satz des Pythagoras und zur Diagonalenberechnung'''< | + | <div style="margin:0px; margin-right:90px; border:thick double green; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; "> |
| + | <span style="color: green">'''Arbeitsauftrag:'''</span> | ||
| + | *Hole dir das '''Übungsblatt zum Kehrsatz zum Satz des Pythagoras und zur Diagonalenberechnung''' | ||
| + | *Berechne die Aufgaben auf dem Blatt | ||
| + | *Vergleiche deine Lösungen mit denen auf der Seite | ||
| + | </div><br /> | ||
== Aufgabe 1== | == Aufgabe 1== | ||
Version vom 24. Januar 2009, 18:32 Uhr
Arbeitsauftrag:
- Hole dir das Übungsblatt zum Kehrsatz zum Satz des Pythagoras und zur Diagonalenberechnung
- Berechne die Aufgaben auf dem Blatt
- Vergleiche deine Lösungen mit denen auf der Seite
Aufgabe 1
a)
- h ist die längste Seite, also müsste sie auch die Hypotenuse sein
- Satz des Pythagoras ansetzen
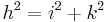
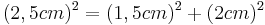
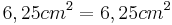
- Der Satz des Pythagoras ist erfüllt
- Das Dreieck ist also rechtwinklig
b)
- k ist die längste Seite, also müsste sie auch die Hypotenuse sein
- Satz des Pythagoras ansetzen
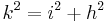
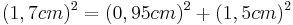
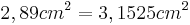
- Der Satz des Pythagoras ist nicht erfüllt, da die Gleichung einen Widerspruch ergibt
- Das Dreieck ist also nicht rechtwinklig
c)
- i ist die längste Seite, also müsste sie auch die Hypotenuse sein
- Satz des Pythagoras ansetzen
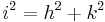
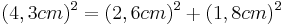
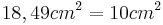
- Der Satz des Pythagoras ist nicht erfüllt, da die Gleichung einen Widerspruch ergibt
- Das Dreieck ist also nicht rechtwinklig
d)
- i ist die längste Seite, also müsste sie auch die Hypotenuse sein
- Satz des Pythagoras ansetzen
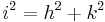
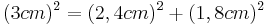
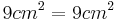
- Der Satz des Pythagoras ist erfüllt
- Das Dreieck ist also rechtwinklig
Aufgabe 2
a)
- Um den Satz des Pythagoras zu testen, muss man zunächst die Länge der fehlenden Seiten berechnen
- Das Dreieck lässt sich in zwei kleinere rechtwinklige Dreiecke zerlegen
- In diesen rechtwinkligen Dreiecken darf man den Satz des Pythagoras ansetzen
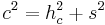
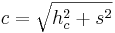
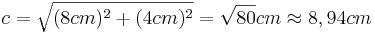
- Da man nun alle Seiten kennt, kann man den Satz des Pythagoras für das Dreieck
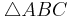 ansetzen
ansetzen
- b ist die längste Seite, also müsste sie die Hypotenuse sein
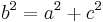
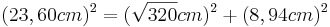
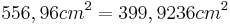
- Der Satz des Pythagoras ergibt einen Widerspruch
- Das Dreieck
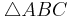 ist also nicht rechtwinklig
ist also nicht rechtwinklig
b)
- Um den Satz des Pythagoras zu testen, muss man zunächst die Länge der fehlenden Seiten berechnen
- Das Dreieck lässt sich in zwei kleinere rechtwinklige Dreiecke zerlegen
- In diesen rechtwinkligen Dreiecken darf man den Satz des Pythagoras ansetzen
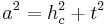
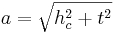
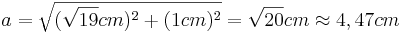
- Da man nun alle Seiten kennt, kann man den Satz des Pythagoras für das Dreieck
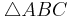 ansetzen
ansetzen
- c ist die längste Seite, also müsste sie die Hypotenuse sein
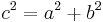
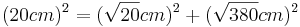
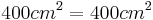
- Der Satz des Pythagoras ergibt eine wahre Aussage
- Das Dreieck
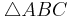 ist also rechtwinklig
ist also rechtwinklig
Aufgabe 3
- Um die Diagonale zu berechnen betrachtet man das rechtwinklige Dreieck
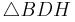
- Die Strecke
![{[BD]\,}](/images/math/3/1/5/3158561b2d57b17461d0b3e196d5263f.png) ist noch unbekannt und man muss sie berechnen
ist noch unbekannt und man muss sie berechnen
- Hierfür betrachtet man das rechtwinklige Dreieck
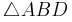
- Man setzt den Satz des Pythagoras an
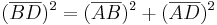
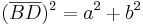
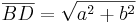
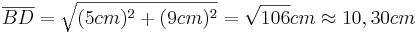
- Damit kann man den Satz des Pythagoras im rechtwinkligen Dreieck
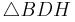 anwenden
anwenden
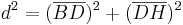

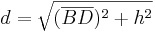
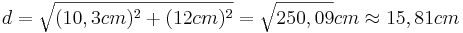
- Die Raumdiagonale d ist also etwa 15,81cm lang
Wenn du fertig gerechnet hast geht es hier zum Ende des Lernpfads.