IV.2. Geraden: Unterschied zwischen den Versionen
Aus RMG-Wiki
| Zeile 81: | Zeile 81: | ||
''IV. Geometrische Grundbegriffe:'' | ''IV. Geometrische Grundbegriffe:'' | ||
<br /> | <br /> | ||
| − | [[P-Seminar/Mathematik 2010-12/IV.1. Geometrische Körper | 1. Geometrische Körper | + | [[P-Seminar/Mathematik 2010-12/IV.1. Geometrische Körper | 1. Geometrische Körper ]] - [[P-Seminar/Mathematik 2010-12/IV.2. Geraden | 2. Geraden]] - [[P-Seminar/Mathematik 2010-12/IV.3. Abstände| 3. Abstände]] - [[P-Seminar/Mathematik 2010-12/IV.4. Parallelogramme - Umfang | 4. Parallelogramm - Umfang]] - [[P-Seminar/Mathematik 2010-12/IV.5. Kreise | 5. Kreise]] - [[P-Seminar/Mathematik 2010-12/IV.6. Winkel | 6. Winkel]] - [[P-Seminar/Mathematik 2010-12/IV.7. Achsensymmetrie | 7. Achsensymmetrie]] - [[P-Seminar/Mathematik 2010-12/IV.8. Netze geometrischer Körper | 8. Netze geometrischer Körper]] - [[P-Seminar/Mathematik 2010-12/IV.9. Schrägbilder | 9. Schrägbilder]]</div></div> |
Version vom 16. April 2013, 13:24 Uhr
IV. Geometrische Grundbegriffe:
Erklärung
- Eine Gerade hat keinen Anfangspunkt und keinen Endpunkt.
- Eine Halbgerade (Strahl) hat einen Anfangspunkt, aber keinen Endpunkt.
- Eine Strecke ist von zwei Punkten begrenzt.
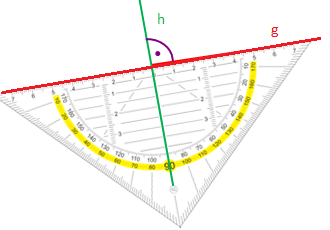
- Liegen zwei Geraden g und h wie im BildaksjjjdfhakdjsfSind zwei Geraden g und h senkrecht zu
- zueinander, so sagt man:aksdfhajjjhhhhhhhhhhhijijikdjsfeiner dritten Gerade k, so sagt man:
- g ist senkrecht zu hakshhhgdfhihihtdfhjijijijijihiakdjsfg und h sind zueinander parallel.
- oder: g ist orthogonal zu h.aksdfhfdvikakhdkjhgfedhijjsfMan schreibt dafür : g||h
- Man schreibt dafür: g
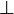 h
h
Aufgaben
1. Richtig oder Falsch? B A
E [AD] 2. Konstruktionsaufgabe 3. Zuordnung
|
IV. Geometrische Grundbegriffe:



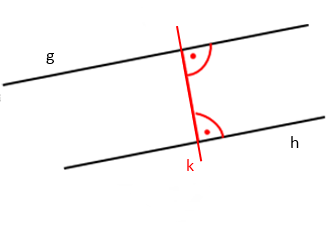
 [AD]
( Richtig)
(!Falsch)
[AD]
( Richtig)
(!Falsch)
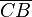 >
> 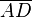 (!Richtig)
(Falsch)
(!Richtig)
(Falsch)
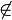 [AD]
(Richtig)
(!Falsch)
[AD]
(Richtig)
(!Falsch)
 [CB
(!Richtig)
(Falsch)
[CB
(!Richtig)
(Falsch)

