IV.3. Abstände: Unterschied zwischen den Versionen
| Zeile 12: | Zeile 12: | ||
<br /> | <br /> | ||
| − | '''Abstand zweier | + | '''Abstand zweier Geraden <span style="color: blue">P</span> und <span style="color: green">Q</span>:'''<br /> |
| − | Die Länge PQ der <span style="color: red">Strecke [PQ] | + | Die Länge PQ der <span style="color: red">Strecke [PQ]</span> <br /> |
| − | + | > PQ = 4 cm<br /> | |
| − | + | ||
<br /> | <br /> | ||
| − | [[Bild:111.png]]<span style="color: | + | [[Bild:111.png]] |
| + | <br /> | ||
| + | '''Abstand eines Punktes <span style="color: blue">P</span> von einer Geraden <span style="color: green">g</span>:'''<br /> | ||
| + | Die Länge der zu <span style="color: green">g</span> <span style="color: purple">senkrechten</span> <span style="color: red">Verbindungsstrecke</span> von P bis g<br /> | ||
| + | > Lösung: 5cm<br /> | ||
| + | <br /> | ||
| + | [[Bild:112.png]] | ||
| + | <br /> | ||
| + | '''Abstand einer Geraden<span style="color: green"> g</span> von einer Geraden <span style="color: blue">h</span>:'''<br /> | ||
| + | Die Länge der zu <span style="color: green">g</span> und <span style="color: blue">h</span> <span style="color: purple">senkrechten</span> <span style="color: red">Verbindungsstrecke</span><br /> | ||
| + | > Lösung: 4cm<br /> | ||
| + | <br /> | ||
| + | [[Bild:113.png]] | ||
| + | <br /> | ||
| + | |||
<br /><br /><br /> | <br /><br /><br /> | ||
<br /> | <br /> | ||
Version vom 16. April 2013, 13:42 Uhr
IV. Geometrische Grundbegriffe:
Erklärung
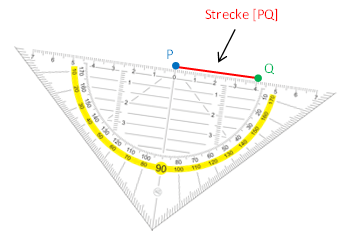
Abstand zweier Geraden P und Q:
Die Länge PQ der Strecke [PQ]
> PQ = 4 cm
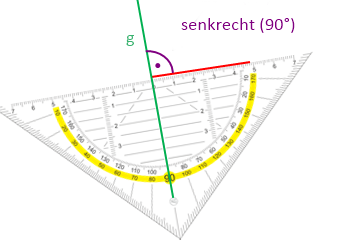
Abstand eines Punktes P von einer Geraden g:
Die Länge der zu g senkrechten Verbindungsstrecke von P bis g
> Lösung: 5cm
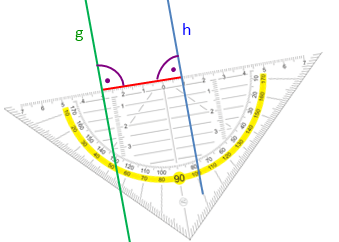
Abstand einer Geraden g von einer Geraden h:
Die Länge der zu g und h senkrechten Verbindungsstrecke
> Lösung: 4cm
Aufgaben
1. Welcher Abstand ist größer? ( Haus - Flugzeug) (! Ball - Flugzeug) (! Flugzeug - Ball) ( Mensch - Haus) ( Flugzeug - Mensch) (! Ball - Mensch) 2. Zeichne die Punkte A(2/3), B(-2/-2), C(5/1) und D(2/0)
Texttexttext einfügen 1 texttexttexttexttext einfügen 2 text.
|
IV. Geometrische Grundbegriffe:
